a) có \(\widehat{DBO}=\widehat{DEO}=90\) độ ( 2 tiếp tuyến )
xét tứ giác BDOE có
\(\widehat{DBO}=\widehat{DEO}=90\) => tứ giác BDOE nội tiếp
b) ta có \(\widehat{ECB}=\widehat{DBE}\) (2 góc nội tiếp (O) chắn \(\stackrel\frown{BE}\) ) (1)
có \(\widehat{DBE}+\widehat{EBO}=90\) độ
lại có \(\widehat{HOB}+\widehat{HBO}=90\) độ
=> \(\widehat{DBE}=\widehat{DOB}\) (2)
lại có \(\widehat{DOB}+\widehat{DOC}=180\) độ (3)
từ (1), (2), (3) ta có
\(\widehat{ECB}+\widehat{DOC}=180\) độ
lại ở vị trí trong cùng phía => EC//DO ( đpcm )
c)
xét ΔAEO và ΔABD có :
\(\widehat{AEO}=\widehat{ABD}=90\) độ
\(\widehat{A}\) chung
=> ΔAEO ∼ ΔABD (g.g)
=> \(\dfrac{AE}{AB}=\dfrac{AO}{AD}\) => AO.AB = AE.AD ( đpcm )

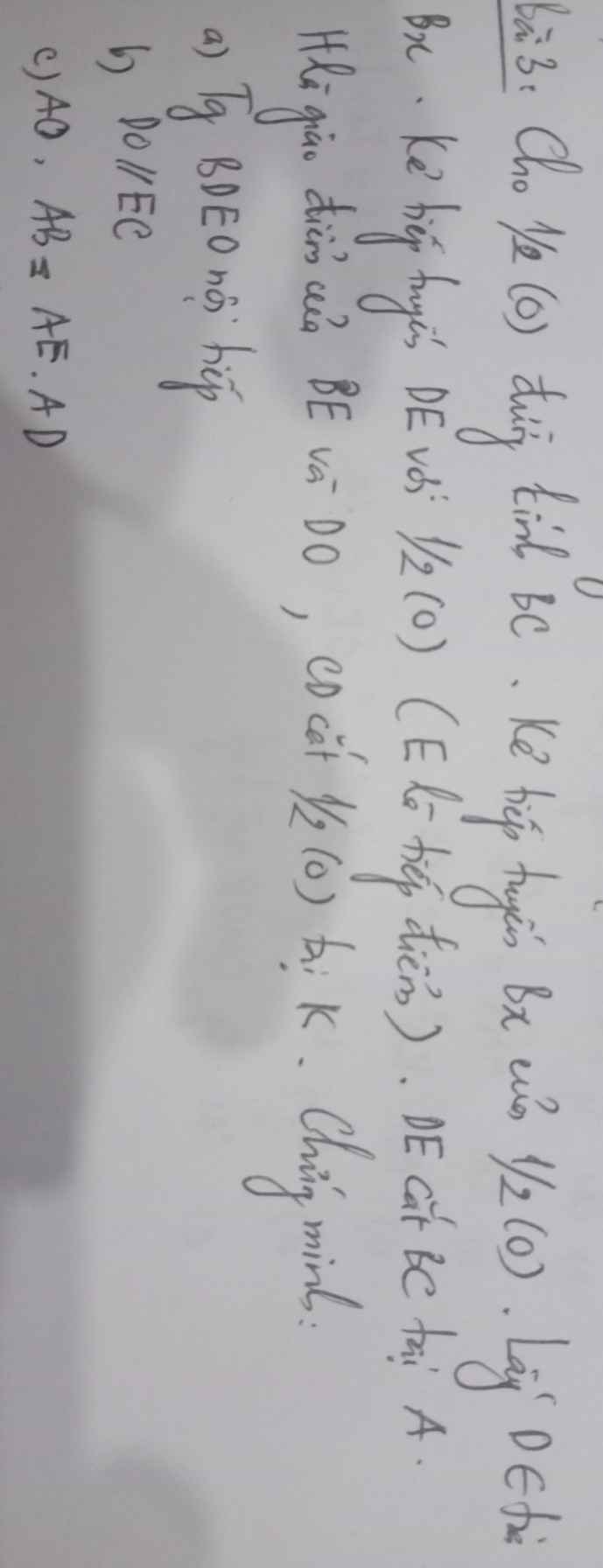





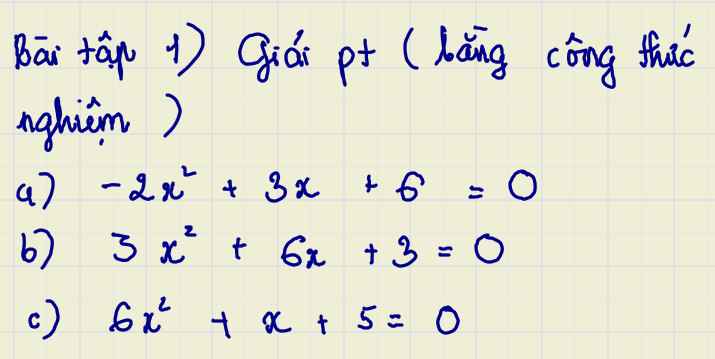







 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)




