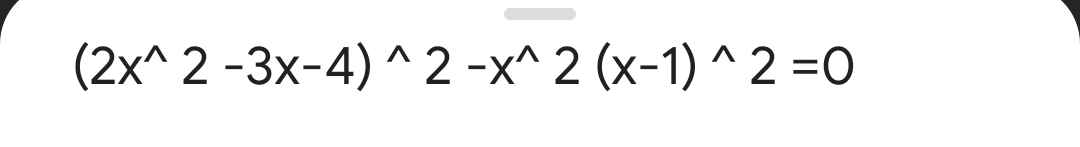\(\Leftrightarrow\left(2x^2-3x-4\right)^2-\left(x^2-x\right)^2=0\\ \Leftrightarrow\left(2x^2-3x-4-x^2+x\right)\left(2x^2-3x-4+x^2-x\right)=0\\ \Leftrightarrow\left(x^2-2x-4\right)\left(3x^2-4x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\left(1\right)\\3x^2-4x-4=0\left(2\right)\end{matrix}\right.\\ \Delta'\left(1\right)=1+4=5\Leftrightarrow x=1\pm\sqrt{5}\\ \Delta'\left(2\right)=4+12=16\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2+4}{3}=2\\x=\dfrac{2-4}{3}=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy ...
(2x2 - 3x - 4)2 - x2(x - 1)2 = 0
<=> (2x2 - 3x - 4)2 = (x2 - x)2
<=> \(\left[{}\begin{matrix}2x^2-3x-4=x^2-x\\2x^2-3x-4=x-x^2\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}\left(x-1-\sqrt{5}\right)\left(x-1+\sqrt{5}\right)=0\\\left(x-2\right)\left(3x+2\right)=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=1\pm\sqrt{5}\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{3}\end{matrix}\right.\end{matrix}\right.\)