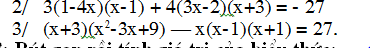- Ta có:
\(f\left(x\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt: \(\left(x^2+5x+5\right)=a\) ta được:
\(=\left(a-1\right)\left(a+1\right)+1\)
\(=a^2-1+1=a^2\)
Thay lại \(a=\left(x^2+5x+5\right)\) được:
\(\left(x^2+5x+5\right)^2\)
- Đối chiếu với \(\left(ax^2+bx+c\right)^2\)
Vậy \(a=1;b=5;c=5\)