2: ΔADE vuông tại D
nên AD<AE
3: h(A;DC)=AD
6: h(C;AD)=CD
7: góc AED<90 độ
=>góc AEF>90 độ
=>AE<AF
2: ΔADE vuông tại D
nên AD<AE
3: h(A;DC)=AD
6: h(C;AD)=CD
7: góc AED<90 độ
=>góc AEF>90 độ
=>AE<AF
Bài 1: Cho hình chữ nhật ABCD, các đường chéo là AC và BD (h.27). Khi đó, do BC vuông góc với Cd nên C là hình chiếu của B trên CD, còn CD là hình chiếu của đường xiên BD trên CD, nên AB< DB
- So sánh AB và BD
- So sánh AD và AC
- Xác định khoảng cách từ điểm D đến đường thẳng BC
Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD:
a) So sánh BH+CK và AB+AC.
b) So sánh BH+CK và BC
Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD:
a) So sánh BH+CK và AB+AC.
b) So sánh BH+CK và BC
Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.
Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.
Bài 2.Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD.
a) So sánh BH+CKvà AB+AC
b) So sánh BH+CKvới BC
1 ) Cho tam giác ABC , D nằm giữa A và C sao cho BD không vuông góc với AC . Gọi E và F là chân các đường vuông góc vẽ từ A và C đến đường thẳng BD . So sánh AD với tổng AE + CF
2 ) Cho tam giác ABC vuông tại A , M là trung điểm của AC . Gọi E và F là chân các đường vuông góc vẽ từ A và C đến đường thẳng BM . Chứng minh rằng : AB < BE + BF / 2
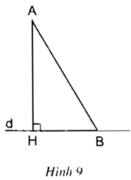
Hãy dùng định lí Py-ta-go để so sánh đường vuông góc AH với đường xiên AB kẻ từ điểm A đến đường thẳng d.
Bài 1: Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E, F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC và tổng AE+CF.