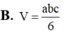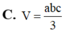Question

1. cho A(1;-1), B(0;6), C(3;-2). Tính \(\overrightarrow{AB}.\overrightarrow{AC}\)

2. cho A(3;-2), B(4;2), C(0;-1). Tính \(\overrightarrow{AB}.\overrightarrow{AC}\)

Answer 1

1: A(1;-1); B(0;6)

=>\(\overrightarrow{AB}=\left(0-1;6+1\right)\)

=>\(\overrightarrow{AB}=\left(-1;7\right)\)

A(1;-1); C(3;-2)

\(\overrightarrow{AC}=\left(3-1;-2+1\right)\)

=>\(\overrightarrow{AC}=\left(2;-1\right)\)

\(\overrightarrow{AB}\cdot\overrightarrow{AC}=\left(-1\right)\cdot2+7\cdot\left(-1\right)=-2-7=-9\)

2: A(3;-2); B(4;2)

=>\(\overrightarrow{AB}=\left(4-3;2+2\right)\)

=>\(\overrightarrow{AB}=\left(1;4\right)\)

A(3;-2); C(0;-1)

\(\overrightarrow{AC}=\left(0-3;-1+2\right)\)

=>\(\overrightarrow{AC}=\left(-3;1\right)\)

\(\overrightarrow{AB}\cdot\overrightarrow{AC}=1\cdot\left(-3\right)+4\cdot1=-3+4=1\)

Answer 2

1. 

`vec{AB} = (0-1;6-(-1)) = (-1;7)`

`vec{AC} = (3-1;-2-(-1)) = (2;-1)`

`=> vec{AB} . vec{AC} = -1.2 + (-1).7 = -9`

2. 

`vec{AB} = (4-3;2-(-2)) = (1;4)`

`vec{AC} = (0-3;-1-(-2)) = (-3;1) `

`=> vec{AB} . vec{AC}= 2 . (-3) + 4.1 = 1`