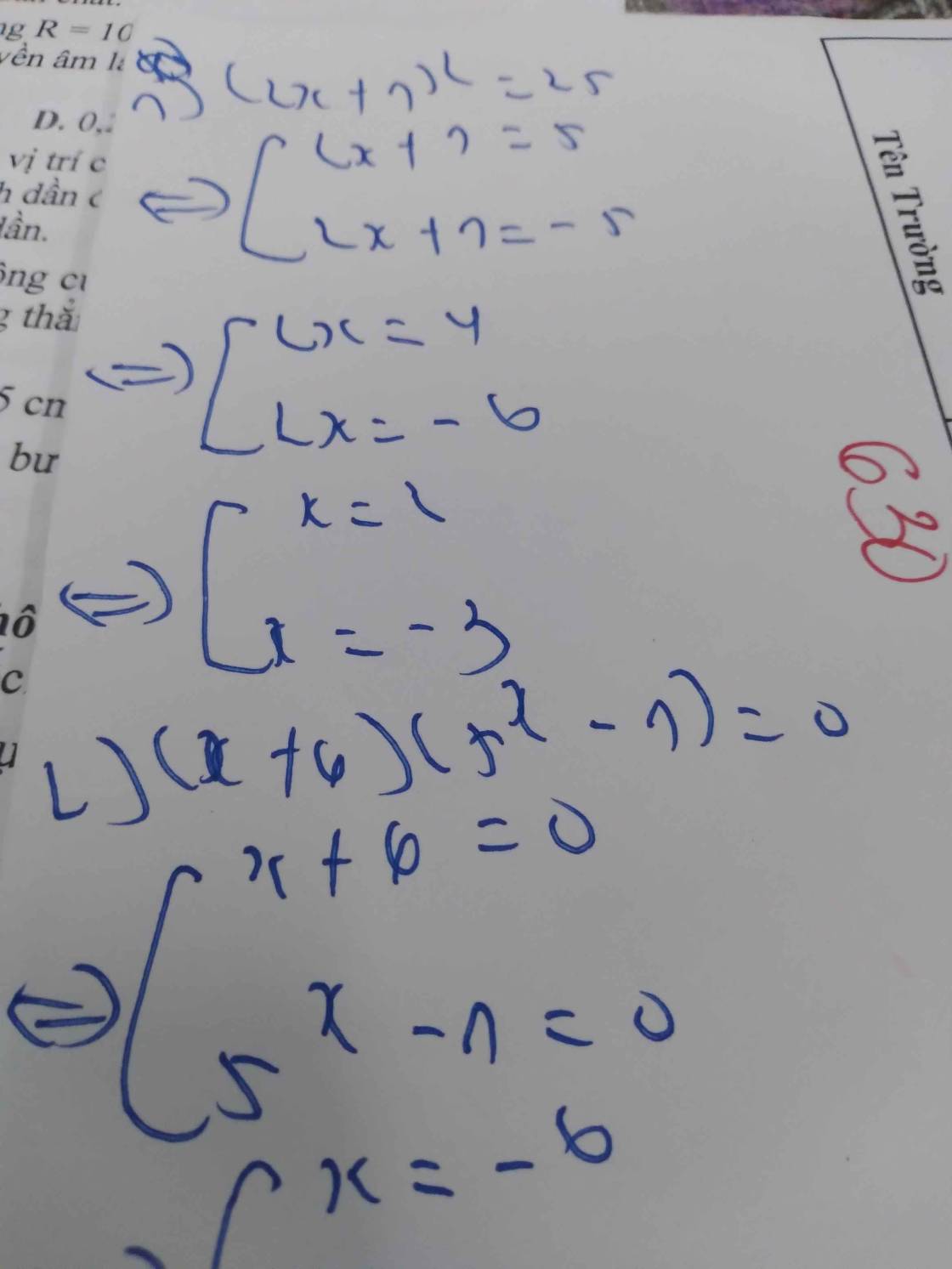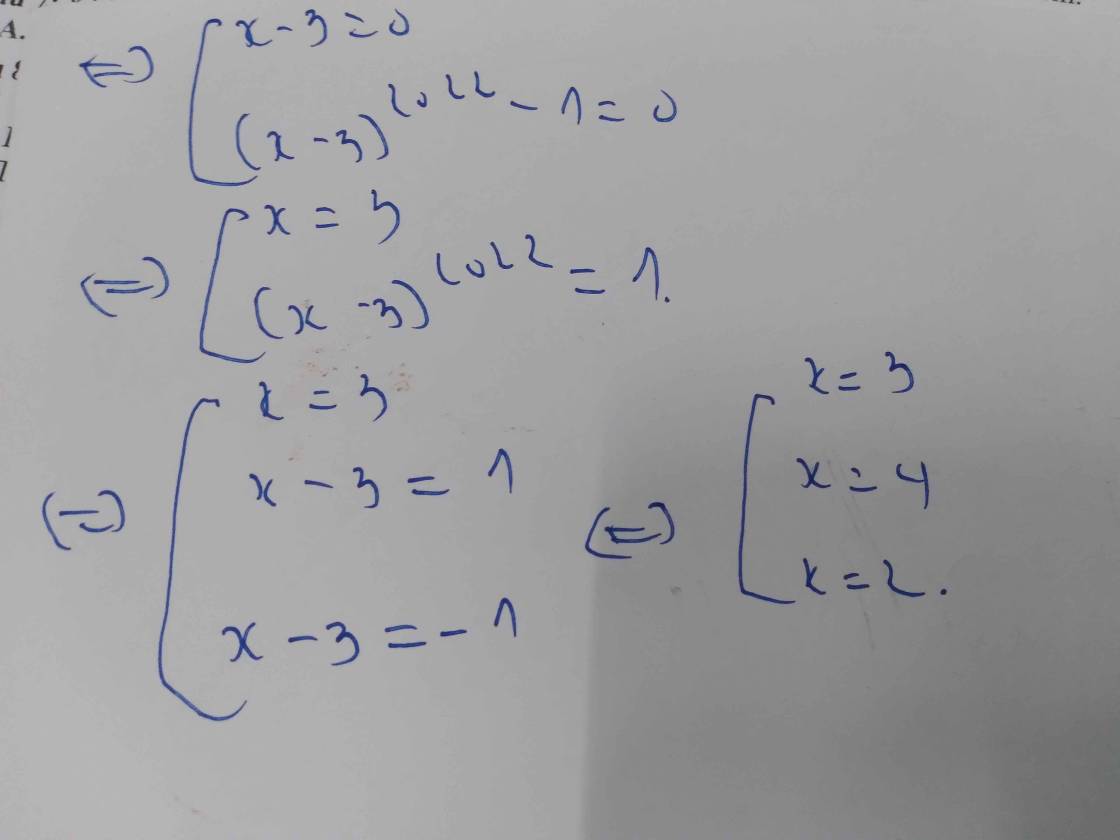`(2^x+1)^2 =25`
`=> (2^x+1)^2 = (+-5)^2`
\(\Rightarrow\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
\(\left(x+6\right)\left(5^x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\5^x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\5^x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=0\end{matrix}\right.\)
\(\left(x-3\right)^{2023}=x-3\)
\(\Rightarrow\left(x-3\right)^{2023}-\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left[\left(x-3\right)^{2022}-1\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x-3=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
`#3107.101107`
1.
`(2^x + 1)^2 = 25`
`=> (2^x + 1)^2 = (+-5)^2`
`=>`\(\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2^x=4\\2^x=-6\left(\text{vô lý}\right)\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
Vậy, `x =2.`
2.
`(x + 6)(5x - 1) = 0`
`=>`\(\left[{}\begin{matrix}x+6=0\\5x-1=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=-6\\5x=1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=-6\\x=\dfrac{1}{5}\end{matrix}\right.\)
Vậy, `x \in {-6; 1/5}`
3.
`2*3^(x + 3) + 3^(2 + x) = 891`
`=> 2* 3^x * 3^3 + 3^2 * 3^x = 891`
`=> 54*3^x + 9*3^x = 891`
`=> 3^x * (54 + 9) = 891`
`=> 3^x * 63 = 891`
`=> 3^x = 891 \div 63`
`=> 3^x = 891/63`
Bạn xem lại đề.
4.
`(x - 3)^2023 = x - 3`
`=> (x - 3)^2023 - (x - 3) = 0`
`=> (x - 3) * [ (x - 3)^2022 - 1] = 0`
`=>`\(\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=\left(\pm1\right)^{2022}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=3\\x-3=1\\x-3=-1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=3\\x=4\\x=2\end{matrix}\right.\)
Vậy, `x \in {2; 3; 4}.`