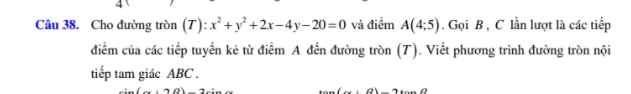Đt (T) có tâm I(-1;2) và R=5
Gọi phương trình tiếp tuyến kẻ từ A đến đt có dạng (d): ax+by+c=0 (a2+b2>0)
Có \(A\in\left(d\right)\Rightarrow4a+5b+c=0\) \(\Leftrightarrow c=-4a-5b\)
Có \(d_{\left(I;d\right)}=R=5\)
\(\Leftrightarrow\dfrac{\left|-a+2b+c\right|}{\sqrt{a^2+b^2}}=5\)\(\Leftrightarrow\dfrac{\left|-a+2b-4a-5b\right|}{\sqrt{a^2+b^2}}=5\)\(\Leftrightarrow\left(-5a-3b\right)^2=25\left(a^2+b^2\right)\)
\(\Leftrightarrow30ab-16b^2=0\) \(\Leftrightarrow\left[{}\begin{matrix}8b=15a\\b=0\end{matrix}\right.\)
TH1:\(8b=15a\)
Chọn \(a=8;b=15\) =>c=-107
=>(d):\(8x+15y-107=0\)
TH2: \(b=0\Rightarrow c=-4a\)
Chọn \(c=-4;a=1\)
=> (d): \(x-4=0\)
Do B và C có vai trò như nhau, giả sử \(B\in\left(d\right):8x+15y-107=0\), \(C\in\left(d\right):x-4=0\)
\(\Rightarrow B\left(15t+4;5-8t\right)\); \(C\left(4;y_c\right)\)
Có \(\left|\overrightarrow{IB}\right|=\left|\overrightarrow{IC}\right|=R\)
\(\Leftrightarrow\sqrt{\left(15t+5\right)^2+\left(3-8t\right)^2}=\sqrt{5^2+\left(y_c-2\right)^2}=5\)
\(\Leftrightarrow\left\{{}\begin{matrix}289t^2+102t+34=25\\25+\left(y_c-2\right)^2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t=-\dfrac{3}{17}\\y_c=2\end{matrix}\right.\) \(\Rightarrow B\left(\dfrac{23}{17};\dfrac{109}{17}\right)\),\(C\left(4;2\right)\)
=> AB=3; AC=3;BC=\(\dfrac{15\sqrt{34}}{17}\)
Áp dụng ct heron tính được diện tích tam giác ABC là: \(S=\dfrac{135}{34}\) (đvdt)
Độ dài bán kính đt nội tiếp tam giác ABC là: \(r=\dfrac{S}{p}\)=...
Gọi E(\(x_E;y_E\)) là tâm đt nội tiếp tam giác ABC
=> \(\overrightarrow{EA}\left(4-x_E;5-y_E\right)\)
\(\overrightarrow{EB}\left(\dfrac{23}{17}-x_E;\dfrac{109}{17}-y_E\right)\); \(\overrightarrow{EC}\left(4-x_E;2-y_E\right)\)
Có \(BC.\overrightarrow{EA}+AB.\overrightarrow{EC}+AC.\overrightarrow{EB}=\overrightarrow{0}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{15\sqrt{34}}{17}.\left(4-x_E\right)+3\left(\dfrac{23}{17}-x_E\right)+3\left(4-x_E\right)=0\\\dfrac{15\sqrt{34}}{17}\left(5-y_E\right)+3\left(\dfrac{109}{17}-y_E\right)+3\left(2-y_E\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_E=\dfrac{273+60\sqrt{34}}{102+15\sqrt{34}}\\y_E=\dfrac{75\sqrt{34}+429}{102+15\sqrt{34}}\end{matrix}\right.\)
(Toi ko bt toi sai hay đề lỗi nhưng toi chỉ làm đến đây, số xấu)