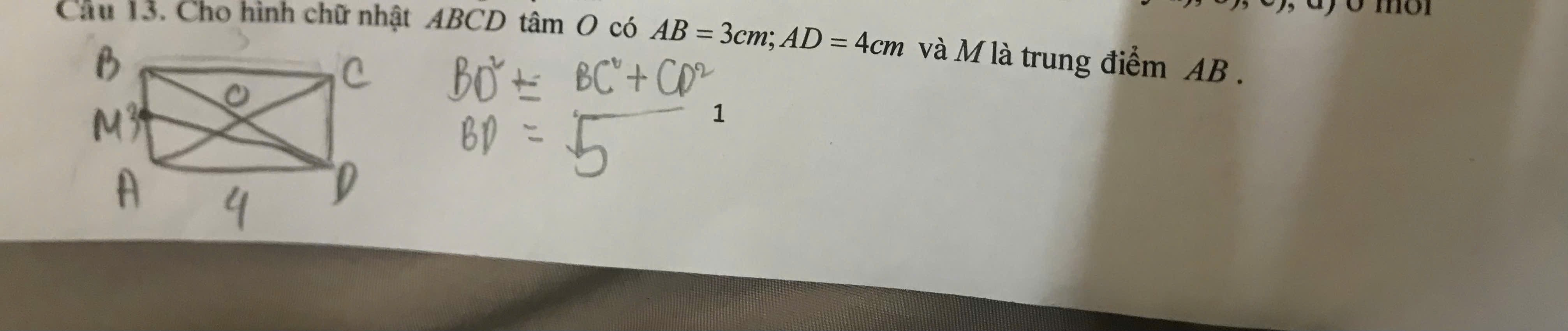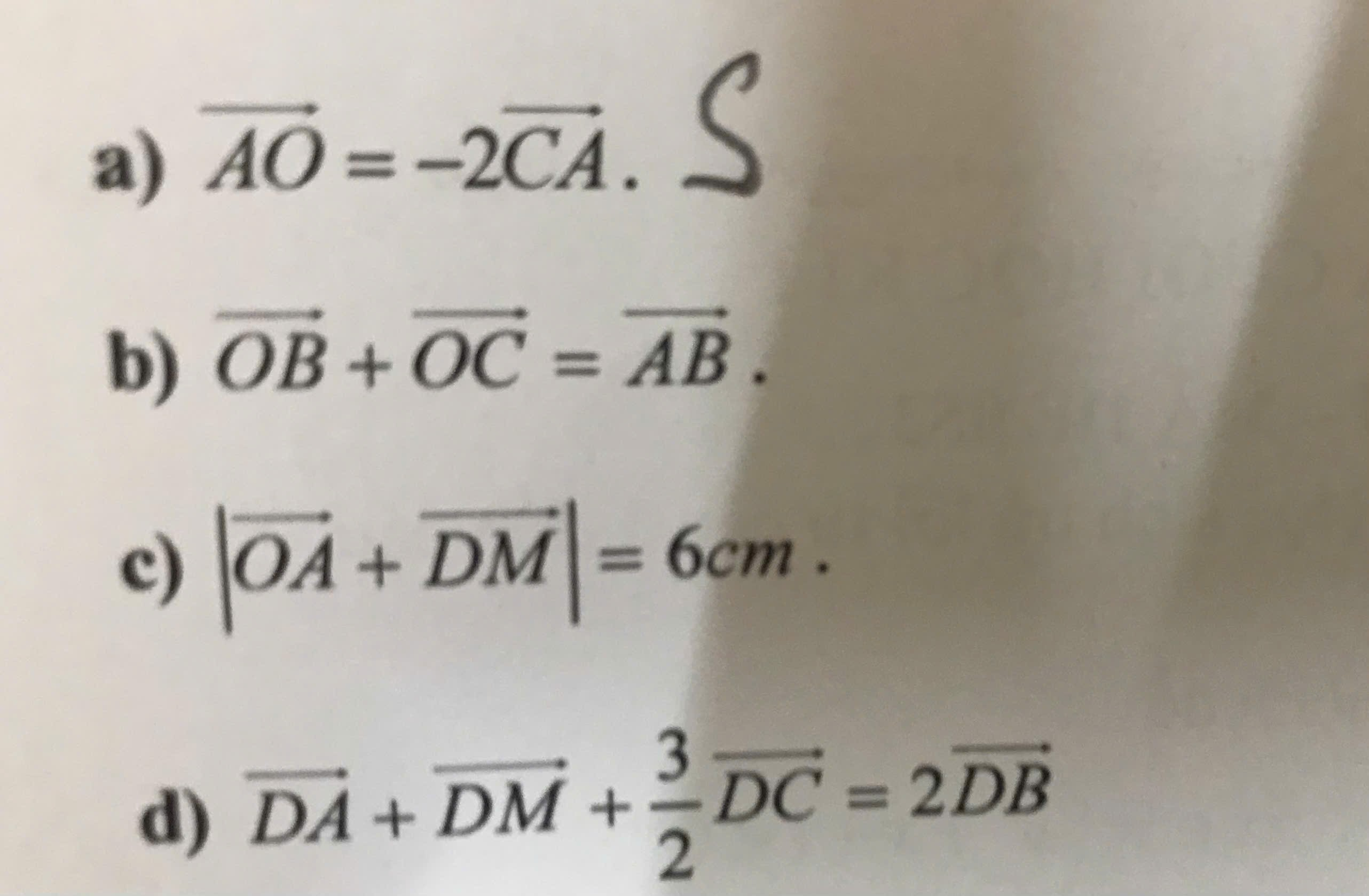a) Sai \(\left(OA=\dfrac{1}{2}AC\right)\)
b) \(\overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{ON}\) (\(N\) là trung điểm \(BC\))
mà \(2\overrightarrow{ON}=\overrightarrow{AB}\) (tính chất Hình chữ nhật)
\(\Rightarrow\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AB}\Rightarrow\) Đúng
c) \(\overrightarrow{DM}=\dfrac{1}{2}\left(\overrightarrow{DB}+\overrightarrow{DA}\right)\) (\(M\) là trung điểm \(AB\))
\(\Rightarrow\overrightarrow{OA}+\overrightarrow{DM}=\overrightarrow{OA}+\dfrac{1}{2}\left(\overrightarrow{DB}+\overrightarrow{DA}\right)=\overrightarrow{OA}+\dfrac{\overrightarrow{DA}-2\overrightarrow{OD}}{2}=\overrightarrow{OA}-\overrightarrow{OD}+\dfrac{1}{2}\overrightarrow{DA}\)
\(\Rightarrow\overrightarrow{OA}+\overrightarrow{DM}=\overrightarrow{DA}+\dfrac{1}{2}\overrightarrow{DA}=\dfrac{3}{2}\overrightarrow{DA}\)
\(\Rightarrow\left|\overrightarrow{OA}+\overrightarrow{DM}\right|=\left|\dfrac{3}{2}\overrightarrow{DA}\right|=\dfrac{3}{2}AD=\dfrac{3}{2}.4=6\left(cm\right)\)
\(\Rightarrow\) Đúng
d) \(\overrightarrow{DA}+\overrightarrow{DM}+\dfrac{3}{2}\overrightarrow{DC}=\overrightarrow{DA}+\dfrac{\overrightarrow{DB}+\overrightarrow{DA}}{2}+\dfrac{3}{2}\overrightarrow{DC}\)
\(=\dfrac{3}{2}\left(\overrightarrow{DA}+\overrightarrow{DC}\right)+\dfrac{\overrightarrow{DB}}{2}=\dfrac{3}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{DB}=2\overrightarrow{DB}=VP\left(đpcm\right)\)
\(\Rightarrow\) Đúng