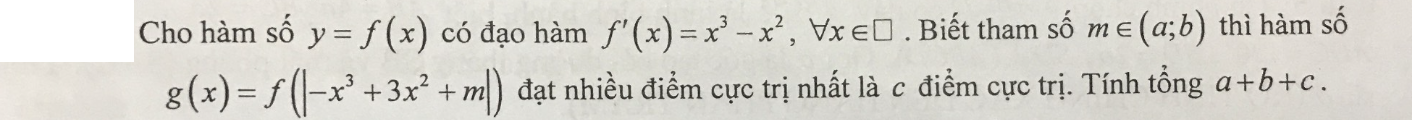\(f\left(x\right)\) có 1 cực trị \(x=1\)
\(u=\left|x^3-3x^2-m\right|\)
- Với \(-4< m< 0\) thì u có 3 nghiệm, với \(\left[{}\begin{matrix}m\ge0\\m\le-4\end{matrix}\right.\) thì u có 1 nghiệm đơn (ko tính nghiệm kép)
BBT hàm u khi u có 3 nghiệm:
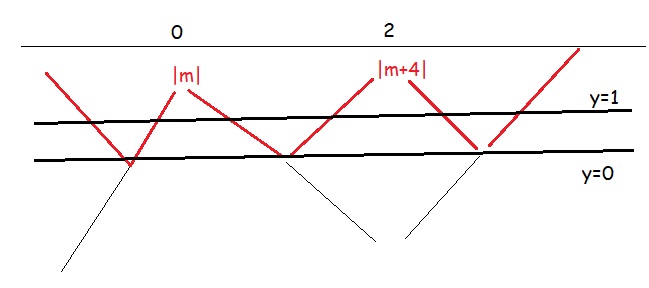
Hàm có nhiều cực trị nhất khi \(\left\{{}\begin{matrix}\left|m\right|>1\\\left|m+4\right|>1\\-4< m< 0\end{matrix}\right.\)
\(\Rightarrow-3< m< -1\)
Khi đó hàm có 11 cực trị
Đúng 1
Bình luận (1)
