Gọi độ dài cạnh hình vuông nhỏ là x với \(0< x< 10\sqrt{2}\)
Độ dài đường chéo hình vuông nhỏ là \(x\sqrt{2}\)
Độ dài cạnh huyền tam giác là \(20-x\sqrt{2}\)
Độ dài cạnh mỗi tam giác là \(\dfrac{20-x\sqrt{2}}{\sqrt{2}}=10\sqrt{2}-x\)
Diện tích lót gạch sẫm màu:
\(x^2+2.\left(10\sqrt{2}-x\right)^2\)
Diện tích còn lại: \(400-x^2-2\left(10\sqrt{2}-x\right)^2\)
Chi phí:
\(f\left(x\right)=0,25.\left[x^2+2\left(10\sqrt{2}-x\right)^2\right]+0,175.\left[400-x^2-2\left(10\sqrt{2}-x\right)^2\right]\)
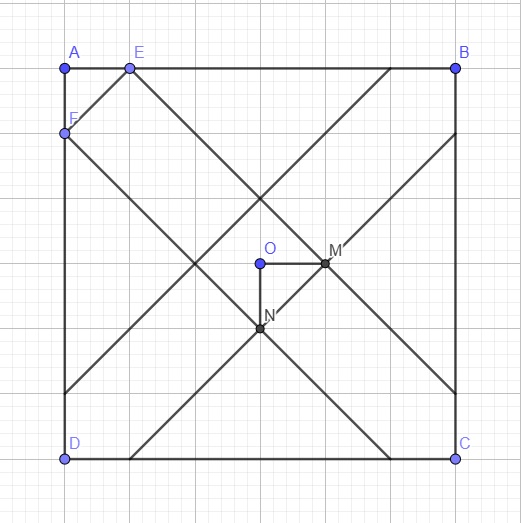
Bài này chỉ cần nhìn ra 2 tam giác OMN và AEF bằng nhau dẫn tới \(OM=AE=\dfrac{x\sqrt{2}}{2}\) là xong









