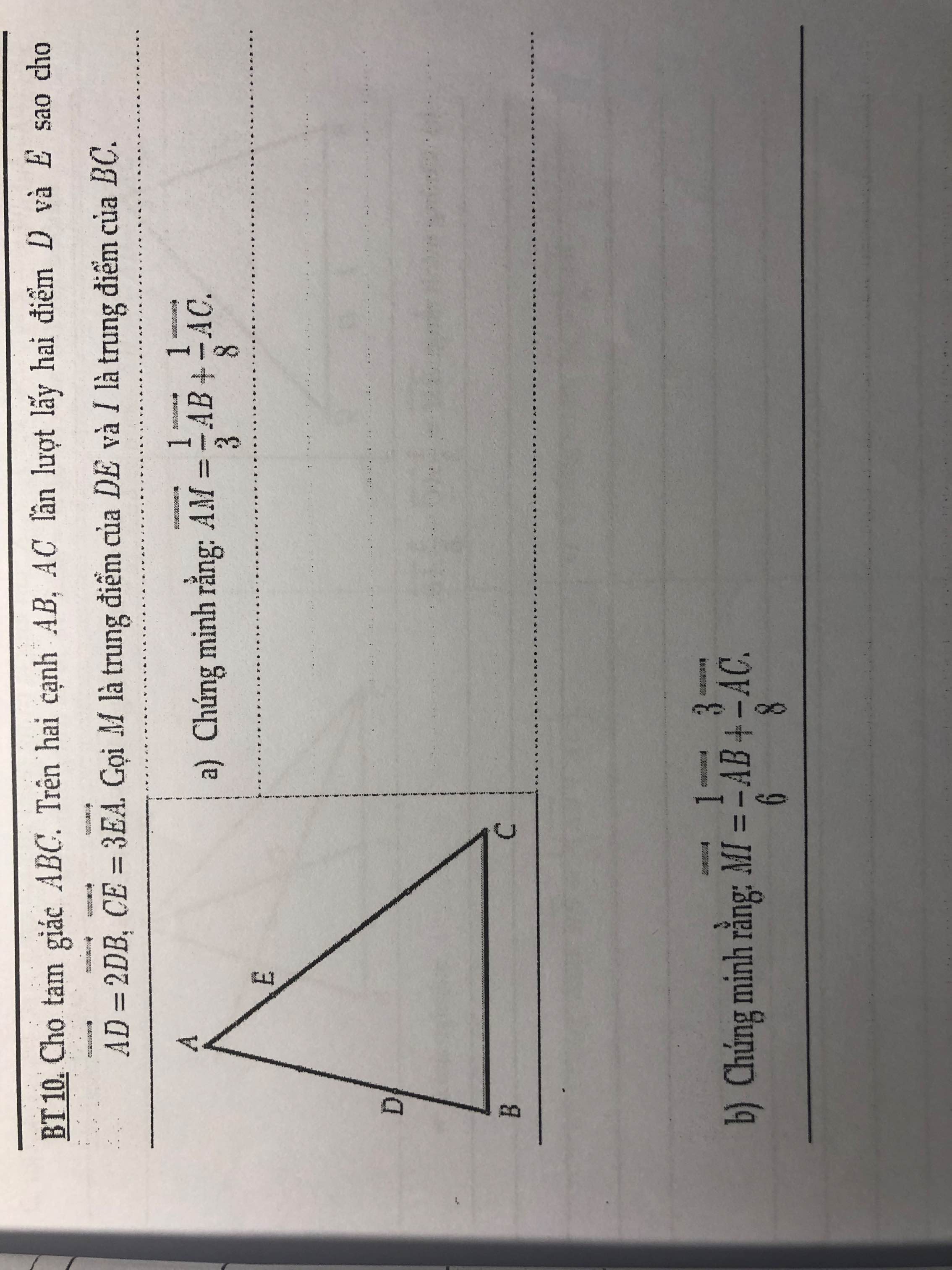
a: \(\overrightarrow{AD}=2\cdot\overrightarrow{DB}\)
=>\(\overrightarrow{AD}=\dfrac{2}{3}\cdot\overrightarrow{AB}\)
\(\overrightarrow{CE}=3\cdot\overrightarrow{EA}\)
=>CE=3EA và E nằm giữa A và C
=>AC=4AE
=>\(\overrightarrow{AE}=\dfrac{1}{4}\cdot\overrightarrow{AC}\)
Xét ΔADE có AM là đường trung tuyến
nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AE}\right)=\dfrac{1}{2}\left(\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\cdot\overrightarrow{AC}\)
b: \(\overrightarrow{MI}=\overrightarrow{MD}+\overrightarrow{DB}+\overrightarrow{BI}\)
\(=\dfrac{1}{2}\cdot\overrightarrow{ED}+\dfrac{1}{3}\cdot\overrightarrow{AB}+\dfrac{1}{2}\cdot\overrightarrow{BC}\)
\(=\dfrac{1}{2}\left(\overrightarrow{EA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\cdot\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\left(-\dfrac{1}{4}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AB}\right)+\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(=-\dfrac{1}{8}\cdot\overrightarrow{AC}+\dfrac{1}{3}\cdot\overrightarrow{AB}+\dfrac{-1}{6}\cdot\overrightarrow{AB}+\dfrac{1}{2}\cdot\overrightarrow{AC}\)
\(=\dfrac{3}{8}\cdot\overrightarrow{AC}+\dfrac{1}{6}\cdot\overrightarrow{AB}\)