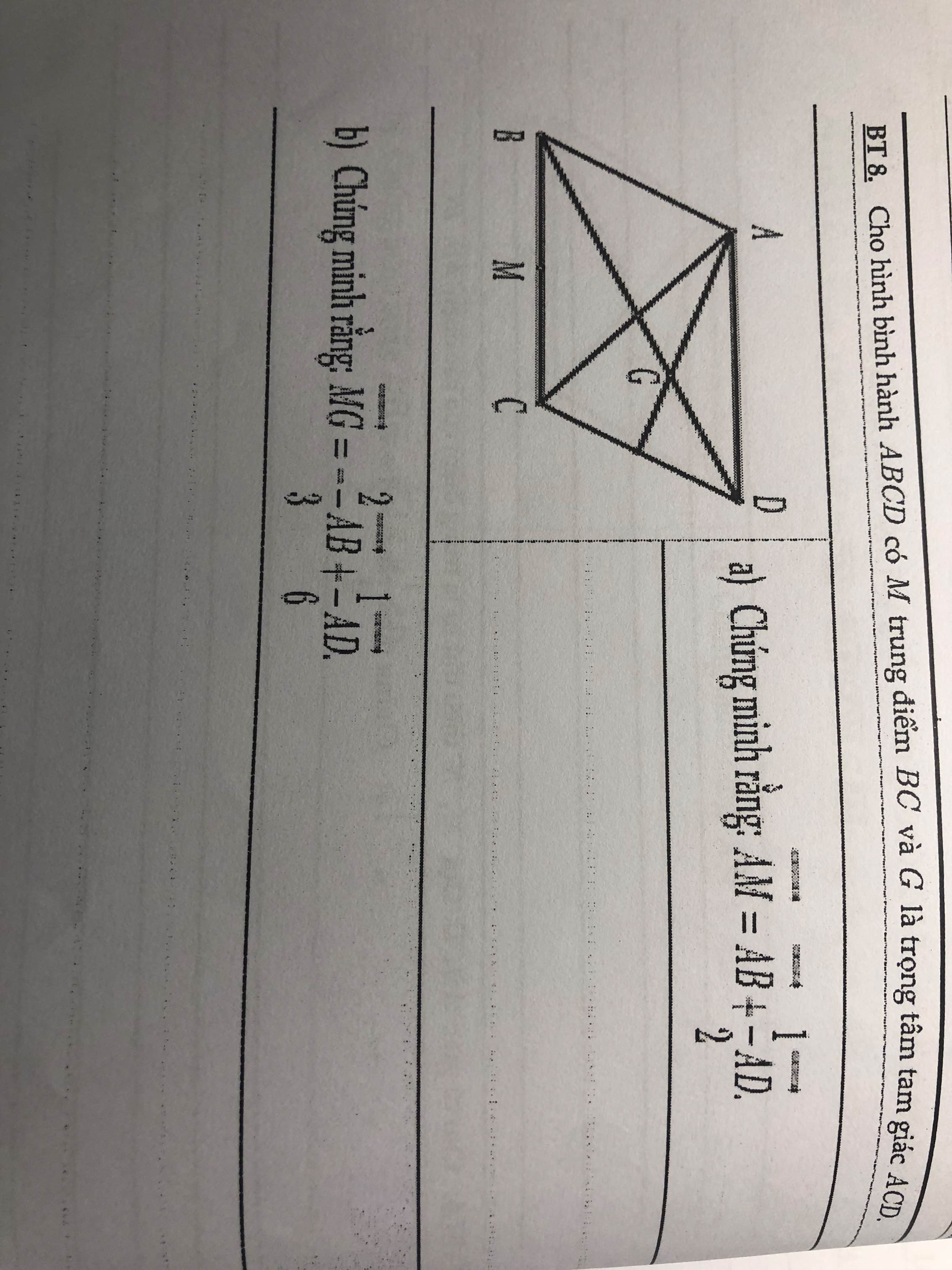
a.
Do M là trung điểm BC nên \(\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{BC}\)
Do ABCD là hình bình hành nên: \(\overrightarrow{AD}=\overrightarrow{BC}\)
Do đó:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
Do G là trọng tâm ACD nên:
\(\overrightarrow{GA}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{GM}+\overrightarrow{MA}\right)+\left(\overrightarrow{GM}+\overrightarrow{MB}\right)+\left(\overrightarrow{GM}+\overrightarrow{MC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(\Leftrightarrow3\overrightarrow{MG}=\overrightarrow{MA}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)+\left(\overrightarrow{MA}+\overrightarrow{AC}\right)\)
\(\Leftrightarrow3\overrightarrow{MG}=3\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{AC}\)
\(\Leftrightarrow3\overrightarrow{MG}=-3\overrightarrow{AM}+\overrightarrow{AB}+\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\)
\(\Leftrightarrow3\overrightarrow{MG}=-3\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)+2\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Leftrightarrow3\overrightarrow{MG}=-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\Leftrightarrow\overrightarrow{MG}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}\)
Đề bài câu này sai