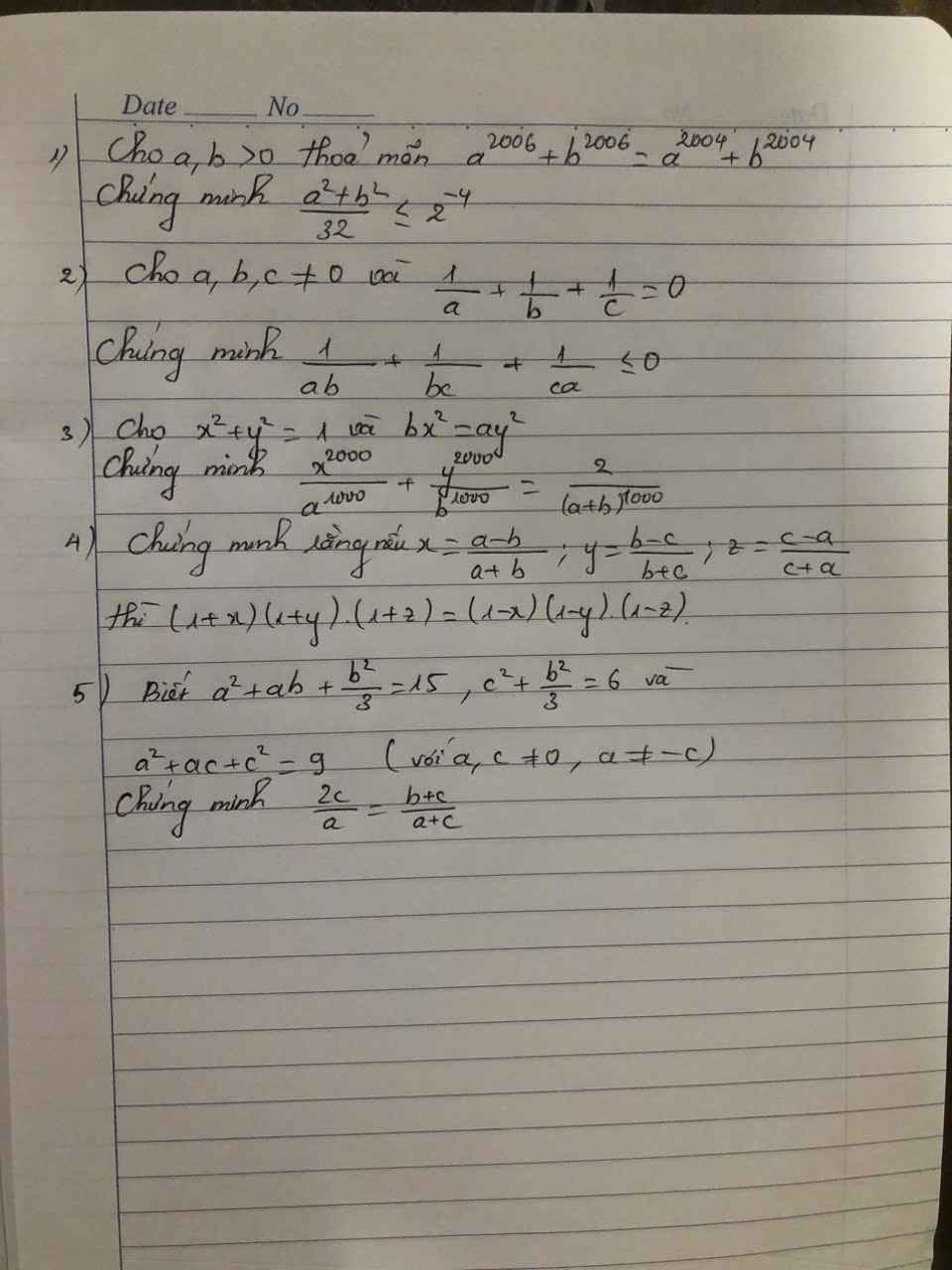Question

Answer 1

bài `2:`

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\\ \left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2=0\\ \dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)=0\\ 2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)=-\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)

`AA a,b,c \ne 0` ta có :

`-(1/a^2 +1/b^2 +1/c^2)<=0`

hay `2(1/(ab)+1/(ac)+1/(bc))<=0`

`=>1/(ab)+1/(bc)+1/(ac)<=0(đpcm)`