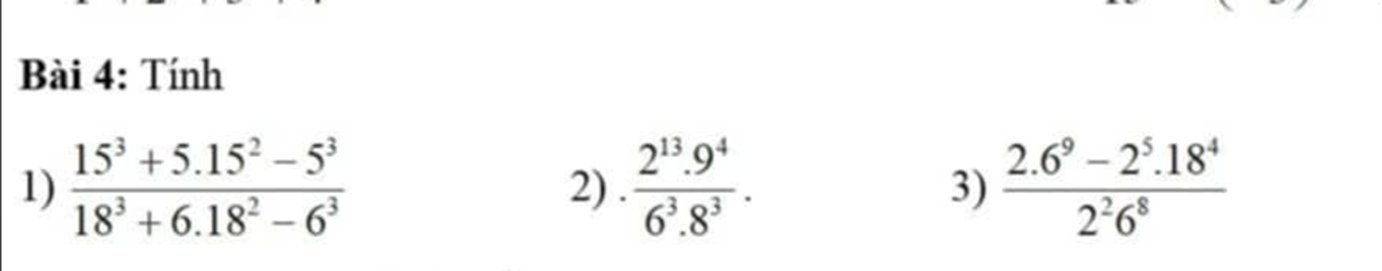1: \(\dfrac{15^3+5\cdot15^2-5^3}{18^3+6\cdot18^2-6^3}=\dfrac{5^3\cdot3^3+5^3\cdot3^2-5^3}{6^3\cdot3^3+6^3\cdot3^2-6^3}=\dfrac{5^3\left(3^3+3^2-1\right)}{6^3\left(3^3+3^2-1\right)}\)
\(=\dfrac{5^3}{6^3}=\dfrac{125}{216}\)
2: \(\dfrac{2^{13}\cdot9^4}{6^3\cdot8^3}=\dfrac{2^{13}\cdot3^8}{2^3\cdot3^3\cdot2^9}=\dfrac{2^{13}}{2^{12}}\cdot\dfrac{3^8}{3^3}=3^5\cdot2=243\cdot2=486\)
3: \(\dfrac{2\cdot6^9-2^5\cdot18^4}{2^2\cdot6^8}=\dfrac{2\cdot2^9\cdot3^9-2^5\cdot2^4\cdot3^8}{2^2\cdot2^8\cdot3^8}\)
\(=\dfrac{2^{10}\cdot3^9-2^9\cdot3^8}{2^{10}\cdot3^8}=\dfrac{2^9\cdot3^8\left(2\cdot3-1\right)}{2^{10}\cdot3^8}=\dfrac{1}{2}\cdot\left(2\cdot3-1\right)=\dfrac{5}{2}\)