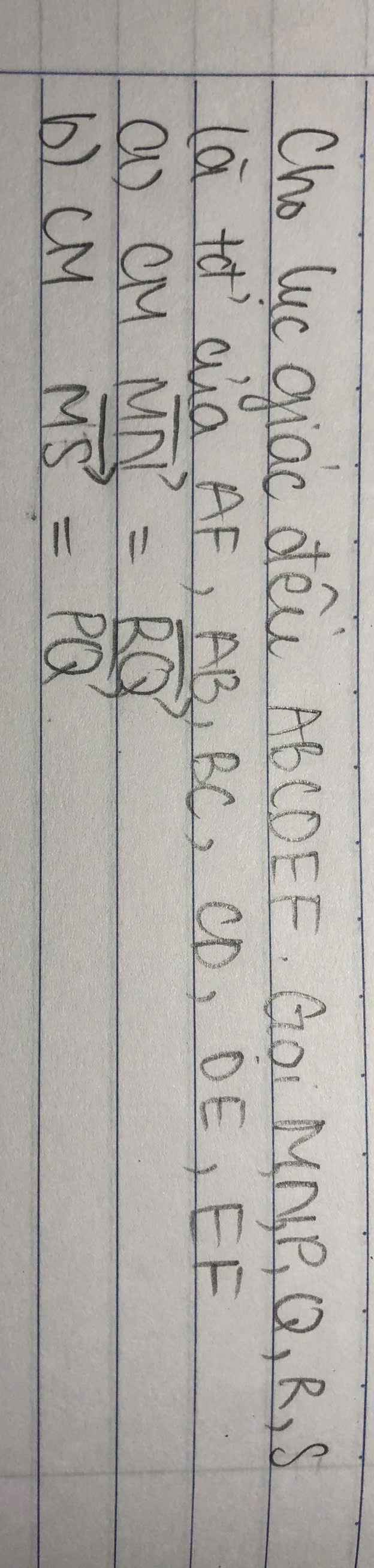a) Có M; N lần lượt là trung điểm của AF; AB
Suy ra MN là đường trung bình của tam giác AFB
\(\Rightarrow MN//BF\); \(MN=\)\(\dfrac{1}{2}BF\) (1)
Chứng minh tương tự: \(RQ//EC;\) \(RQ=\dfrac{1}{2}EC\) (2) (do RQ là đường trung bình của tam giác DEC)
Các góc trong hình lục giác đều có số đo bằng \(120^0\)
\(\Rightarrow\widehat{A}=\widehat{D}=120^0\)
Tam giác AFB và DEC cân tại A và D \(\Rightarrow\widehat{AFB}=\widehat{ABF}=\widehat{DEC}=\widehat{DCE}E=30^0\)
\(\Rightarrow\widehat{BFE}=\widehat{FBC}=\widehat{FEC}=\)\(120^0-30^0=90^0\)
Suy ra FBCE là hình chữ nhật (tứ giác có ba góc vuông)
\(\Rightarrow FB//EC\); \(FB=EC\) (3)
Từ (1)(2)(3) \(\Rightarrow MN//RQ\), \(MN=RQ\)
\(\Rightarrow\overrightarrow{MN}=\overrightarrow{RQ}\left(dpcm\right)\)
b) Làm tương tự ý a.