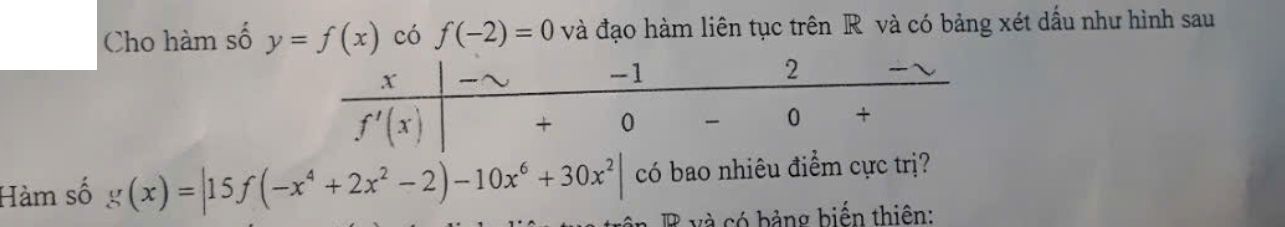\(h\left(x\right)=15f\left(-x^4+2x^2-2\right)-10x^6+30x^2\)
\(h'\left(x\right)=15.\left(-4x^3+4x\right).f'\left(-x^4+2x^2-2\right)-60x^5+60x\)
\(=-60x.\left(x^2-1\right)\left[f'\left(-x^4+2x^2-2\right)+x^2+1\right]\)
Xét \(f'\left(-x^4+2x^2-2\right)+x^2+1=0\)
Do \(u=-x^4+2x^2-2=-1-\left(x^2-1\right)^2\le-1;\forall x\)
Nên từ BBT ta thấy \(f'\left(u\right)\ge0\)
Đồng thời \(x^2+1>0\)
\(\Rightarrow f'\left(-x^4+2x^2-2\right)+x^2+1>0;\forall x\)
\(\Rightarrow h'\left(x\right)=0\) chỉ có 3 nghiệm \(-1;0;1\)
BBT h(x):
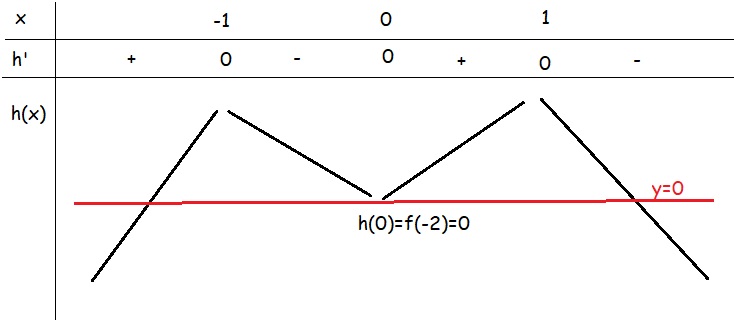
Từ BBT thấy \(y=0\) cắt \(h\left(x\right)\) tại 2 điểm phân biệt (và 1 điểm tiếp xúc)
Nên g(x) có 5 cực trị
Đúng 2
Bình luận (1)
