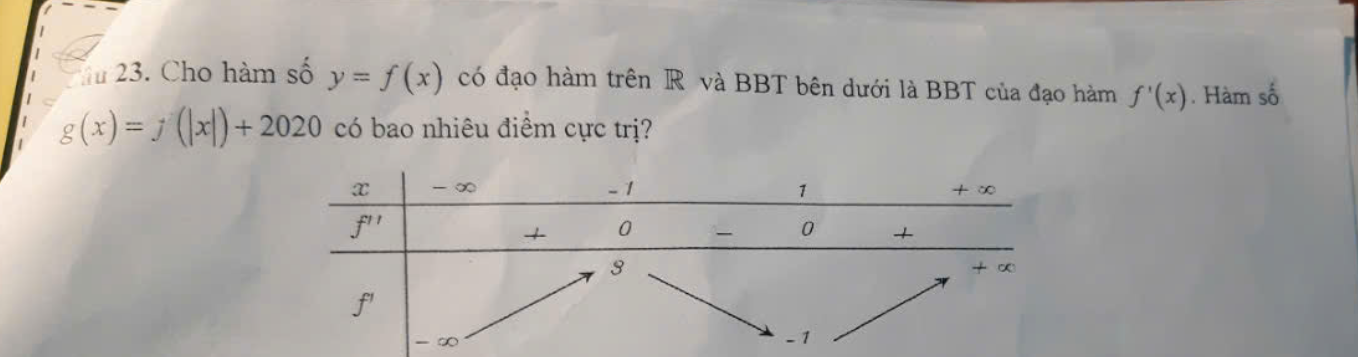
Bài này đành nghịch suy thôi, chỉ nhìn BBT ko phán xét được
\(f''\left(x\right)=k.\left(x-1\right)\left(x+1\right)=k\left(x^2-1\right)\)
\(\Rightarrow f'\left(x\right)=k\left(\dfrac{x^3}{3}-x\right)+C\)
Thay 2 tọa độ (-1;8) (số này là 8 hay 3?) và (1;-1) vào ta được \(\left\{{}\begin{matrix}k=\dfrac{27}{4}\\C=\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)=\dfrac{27}{4}\left(\dfrac{x^3}{3}-x\right)+\dfrac{7}{2}\)
Bấm máy thấy 3 nghiệm trong đó có 2 nghiệm dương
Vậy g(x) có 5 cực trị
Đúng 2
Bình luận (0)
