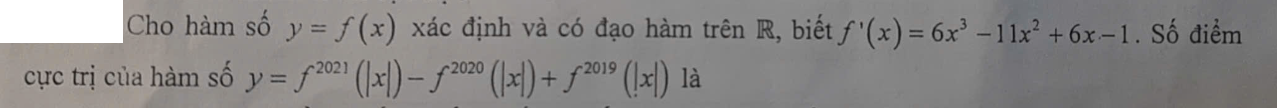\(f'\left(x\right)=0\) có 3 nghiệm 1/2, 1/3, 1 đều dương
\(u=\left|x\right|\)
\(y'=u'.f'\left(u\right).\left[2021.f^{2020}\left(u\right)-2020.f^{2019}\left(u\right)+2019.f^{2018}\left(u\right)\right]\)
\(=u'.f'\left(u\right).f^{2018}\left(u\right).\left[2021.f^2\left(u\right)-2020.f\left(u\right)+2019\right]\)
Pt \(2021t^2-2020t+2019=0\) vô nghiệm
\(f^{2018}\left(u\right)\) bậc chẵn nên ko ảnh hưởng cực trị
\(u'.f'\left(u\right)\) về bản chất chính là \(\left[f\left(\left|x\right|\right)\right]'\)
Nên số cực trị của \(y\) và \(f\left(\left|x\right|\right)\) là như nhau
\(\Rightarrow3.2+1=7\) cực trị
Trên lớp cô chỉ dạy cơ bản rồi cho làm đề, rồi cô gọi nên bảng chữa, cô không đi sâu vào hướng làm, mà chỉ gọi học sinh nên chữa rồi giảng bài đã chữa đó, mà mỗi người có 1 tư duy khác nhau không biết sai/ đúng thế nào.
\(\Rightarrow\) ĐỒNG HƯƠNG - VÀ TUI ĐANG KHÓK THÉT