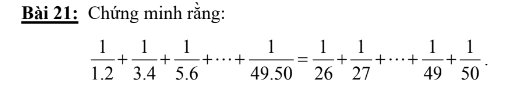\(\dfrac{1}{1\cdot2}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{49\cdot50}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}\right)-2\cdot\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
\(=1+\dfrac{1}{2}+...+\dfrac{1}{50}-1-\dfrac{1}{2}-...-\dfrac{1}{25}\)
\(=\dfrac{1}{26}+\dfrac{1}{27}+\dfrac{1}{28}+...+\dfrac{1}{50}\)
Đúng 1
Bình luận (0)
