Question

Answer 1

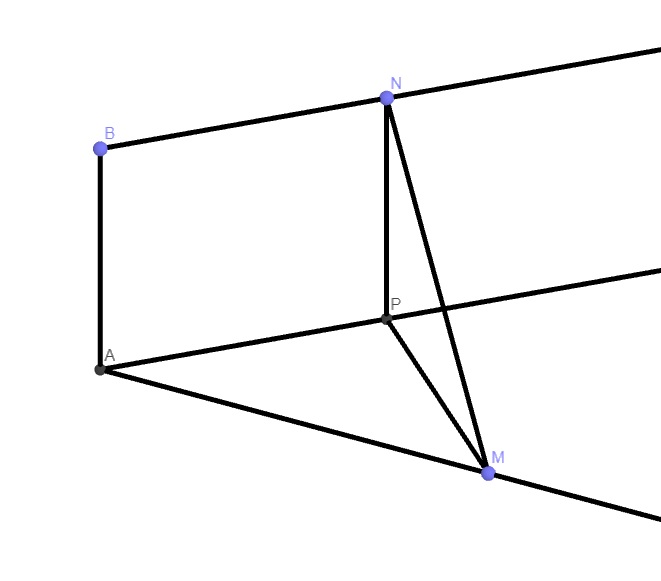
Qua A kẻ đường thẳng d song song BN, từ N kẻ \(NP\perp d\) \(\Rightarrow\widehat{MAP}=\varphi\)

Trong tam giác vuông MNP: \(MP^2=MN^2-NP^2=c^2-AB^2\)

Trong tam giác AMP:

\(MP^2=AP^2+AM^2-2AP.AM.cos\varphi\)

\(\Rightarrow c^2-AB^2=AP^2+AM^2-2AP.AM.cos\varphi\)

\(\Rightarrow c^2-AB^2=BN^2+AM^2-2BN.AM.cos\varphi\ge2BN.AM-2BN.AM.cos\varphi\)

\(\Rightarrow c^2-AB^2\ge BN.AM.2\left(1-cos\varphi\right)\)

\(\Rightarrow BN.AM\le\dfrac{c^2-AB^2}{2\left(1-cos\varphi\right)}\)

Answer 2

Answer 3

Làm gần xong mới nhận ra \(AM,BN\) ở đề bài đúng ra phải là \(AM.BN\)