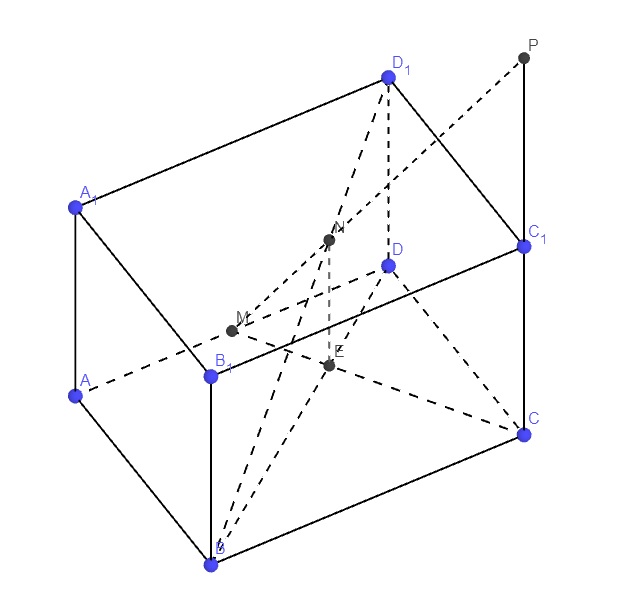
\(\left\{{}\begin{matrix}M\in CM\\P\in CC_1\end{matrix}\right.\) \(\Rightarrow MP\in\left(NCC_1\right)\)
M, N, P thẳng hàng \(\Rightarrow N\in MP\in\left(MCC_1\right)\)
\(\Rightarrow N=BD_1\cap\left(MCC_1\right)\)
Dựa vào đó dựng hình
Trong mp (ABCD), gọi E là giao điểm BC và MD
\(\dfrac{ME}{EC}=\dfrac{MD}{BC}=\dfrac{1}{2}\) (Thales)
Trong mp \(\left(BDD_1\right)\), qua E kẻ đường thẳng song song \(DD_1\) cắt \(BD_1\) tại N
Trong mp \(\left(MCC_1\right)\), nối MN kéo dài cắt \(CC_1\) tại P
Thales: \(\dfrac{MN}{NP}=\dfrac{ME}{EC}=\dfrac{1}{2}\)
Đúng 1
Bình luận (1)
