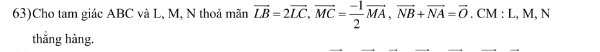\(2\overrightarrow{LC}=\overrightarrow{LB}=\overrightarrow{LC}+\overrightarrow{CB}\Rightarrow\overrightarrow{CL}=\overrightarrow{BC}\)
\(\overrightarrow{MC}=-\dfrac{1}{2}\overrightarrow{MA}=-\dfrac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{CA}\right)\Rightarrow\overrightarrow{MC}=\dfrac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{NB}+\overrightarrow{NA}=\overrightarrow{0}\Rightarrow\overrightarrow{AN}=\overrightarrow{NB}=\overrightarrow{NA}+\overrightarrow{AB}=-\overrightarrow{AN}+\overrightarrow{AB}\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}\)
Từ đó:
\(\overrightarrow{ML}=\overrightarrow{MC}+\overrightarrow{CL}=\dfrac{1}{3}\overrightarrow{AC}+\overrightarrow{BC}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=-2\overrightarrow{MC}+\dfrac{1}{2}\overrightarrow{AB}=-\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{6}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BC}\)
\(=-\dfrac{1}{2}\left(\dfrac{1}{3}\overrightarrow{AC}+\overrightarrow{BC}\right)=-\dfrac{1}{2}\overrightarrow{ML}\)
\(\Rightarrow L,M,N\) thẳng hàng