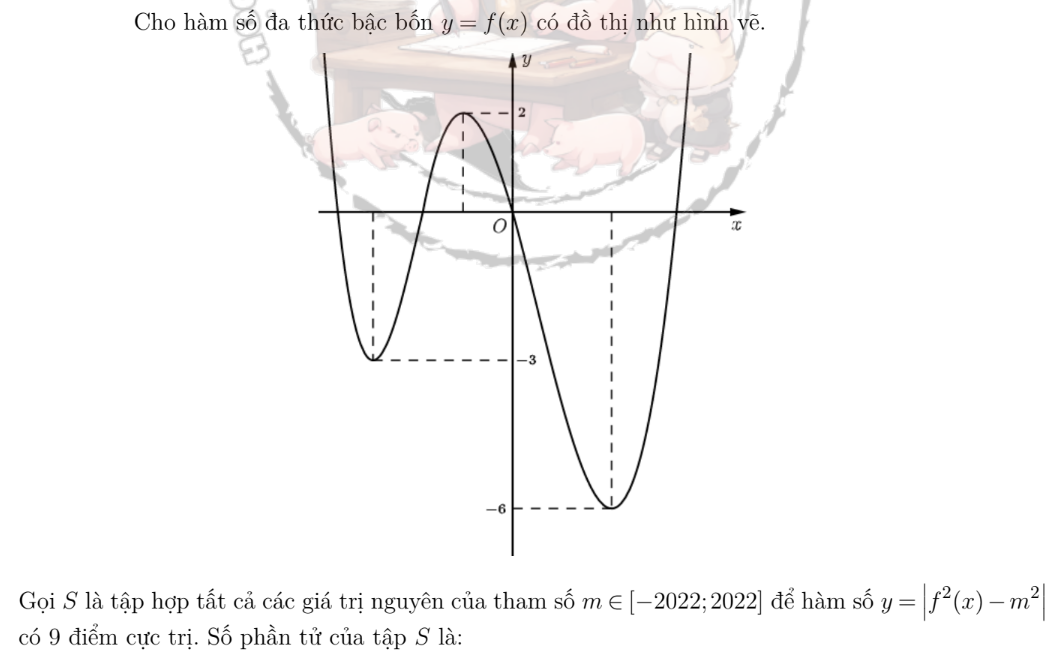
\(g\left(x\right)=f^2\left(x\right)-m^2\)
\(g'\left(x\right)=2f\left(x\right).f'\left(x\right)=0\)
\(f\left(x\right)=0\) cho 4 nghiệm, \(f'\left(x\right)=0\) cho 3 nghiệm
\(\Rightarrow g\left(x\right)=0\) cho 2 nghiệm
\(g\left(x\right)=0\Rightarrow f^2\left(x\right)-m^2=0\Rightarrow\left[{}\begin{matrix}f\left(x\right)=m\\f\left(x\right)=-m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m>0\\m\ge2\\-m\le-6\end{matrix}\right.\) \(\Rightarrow m\ge6\)
Hoặc \(\left\{{}\begin{matrix}m< 0\\-m\ge2\\m\le-6\end{matrix}\right.\) \(\Rightarrow m\le-6\)
Vậy \(\left[{}\begin{matrix}m\ge6\\m\le-6\end{matrix}\right.\)
Đúng 3
Bình luận (3)
