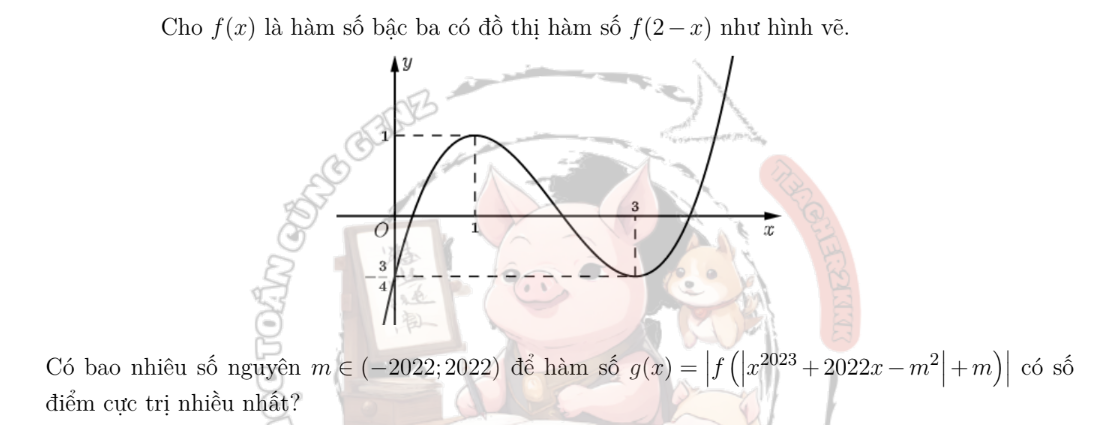
Nhìn số to to thấy ớn quá, dù nó cũng chỉ là ghép trục
Thấy ngay là \(u=x^{2023}+2022x-m^2\) luôn đồng biến nên BBT hàm \(h=\left|x^{2023}+2022x-m^2\right|+m\) có dạng:
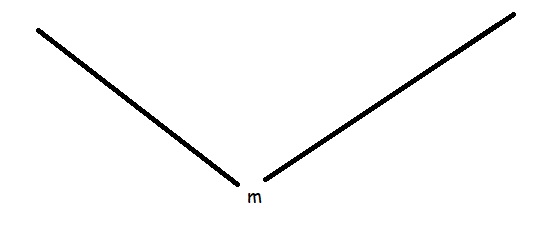
\(\Rightarrow g\left(x\right)\) có nhiều cực trị nhất khi:
\(y=-1;1\) cắt h tại 2 điểm \(\Rightarrow m< -1\)
\(h=x_1;x_2;x_3\) (với \(x_1>x_2>x_3=-1\) là nghiệm của \(f\left(x\right)=0\) có nhiều nghiệm nhất
\(\Rightarrow m< -1\)
Vậy \(m< -1\)
Đúng 2
Bình luận (0)
