g(x) xác định khi \(x\in\left(-2;2\right)\)
\(g'=f'\left(x+1\right)+\dfrac{4k}{x^2-4}+x+3+\dfrac{4}{x-2}\) với \(k=\dfrac{2020}{m}\)
\(\Rightarrow f'\left(x+1\right)=\dfrac{4k}{4-x^2}+\dfrac{4}{2-x}-x-3\)
\(h\left(x\right)=\dfrac{4k}{4-x^2}+\dfrac{4}{2-x}-x-3\)
\(h'\left(x\right)=\dfrac{x\left[8m+\left(4-x\right)\left(x+2\right)^2\right]}{\left(4-x^2\right)^2}\)
Do m nguyên dương và \(-2< x< 2\) nên thấy ngay \(8m+\left(4-x\right)\left(x+2\right)^2>0\)
BBT h(x):
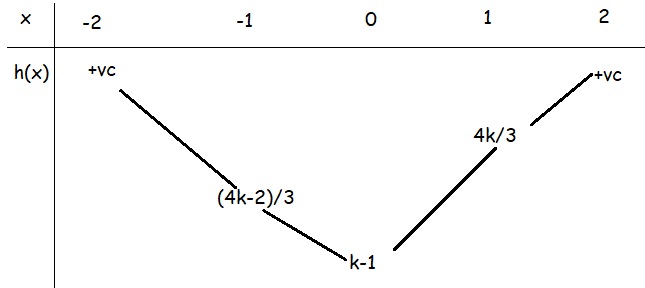
Hàm nghịch biến trên khoảng đã cho khi \(\max\limits_{\left(-1;1\right)}f'\left(x+1\right)=4\le\min\limits_{\left(-1;1\right)}h\left(x\right)=k-1\)
\(\Rightarrow k\ge5\)
\(\Rightarrow\dfrac{2020}{m}\ge5\Rightarrow m\le404\)
Server lỗi làm đi làm lại tới 3 lần, nản thật chứ









