\(h\left(x\right)=f\left(\sqrt{x^2+1}\right)+x^2\)
\(u=\sqrt{x^2+1}\Rightarrow x^2=u^2-1\)
\(u'=0\Rightarrow x=0\)
\(h\left(u\right)=f\left(u\right)+u^2-1=0\Rightarrow h'\left(u\right)=f'\left(u\right)+2u\)
Từ đồ thị \(\Rightarrow h'\left(u\right)=0\) có đúng 1 nghiệm \(u=2\)
\(\Rightarrow x=\pm\sqrt{3}\)
\(h\left(0\right)=f\left(1\right)< 0\)
BBT hàm \(h\left(x\right)\)
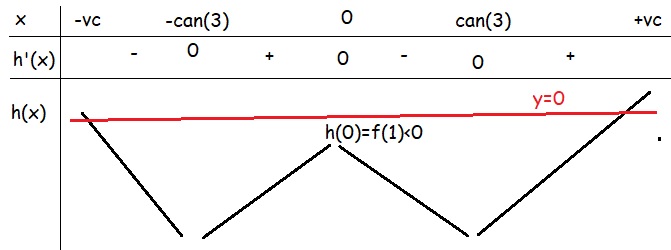
Từ BBT \(\Rightarrow h\left(x\right)=0\) có 2 nghiệm pb
Từ đó chỉ có thể kết luận hàm đồng biến trên \(\left(0;\sqrt{3}\right)\) là chắc chắn, 2 khoảng ĐB còn lại ko thể xác định chính xác nghiệm của \(h\left(x\right)=0\Rightarrow\) ko thể biết cụ thể được nghiệm









