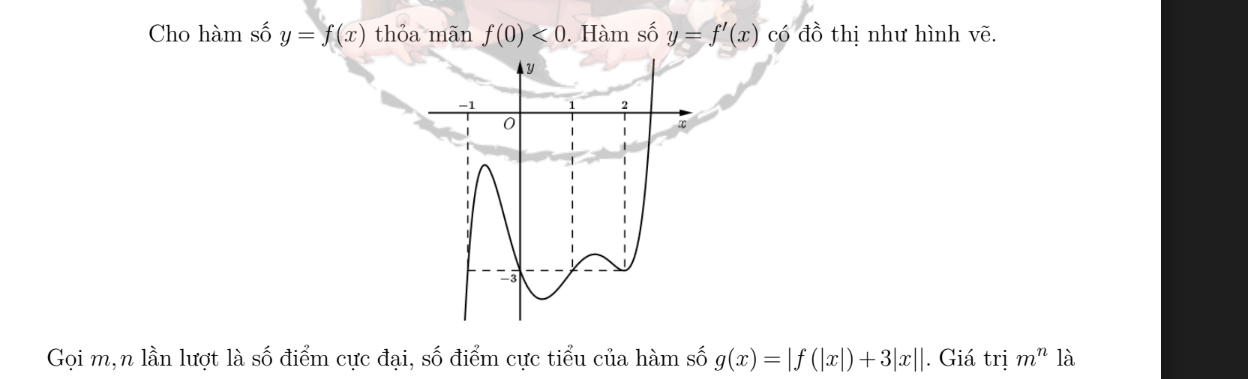
\(h\left(x\right)=f\left(\left|x\right|\right)+3\left|x\right|\)
\(u=\left|x\right|\ge0\)
\(h\left(u\right)=f\left(u\right)+3u\Rightarrow h'=f'\left(u\right)+3\)
\(\Rightarrow h'=0\) có 3 nghiệm \(u=-1\) (loại), \(0;1\), 2(kép => loại)
BBT u:
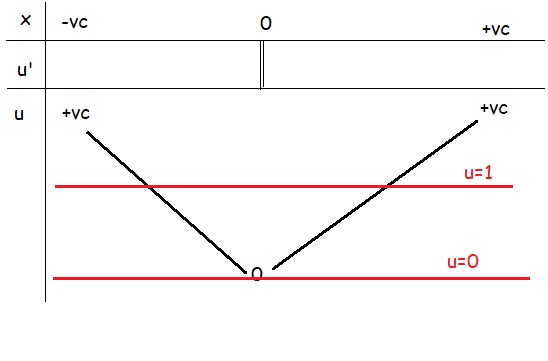
\(\Rightarrow h\left(x\right)\) có 3 cực trị
BBT hàm \(h\left(x\right)\)
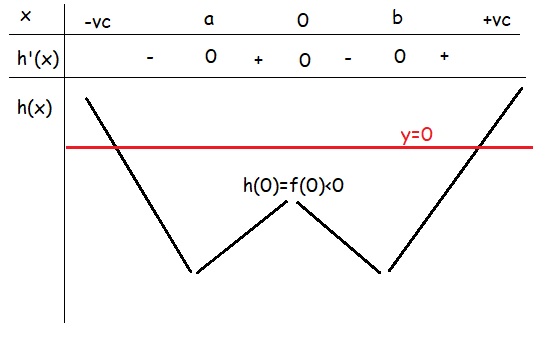
\(\Rightarrow h\left(x\right)=0\) có 2 nghiệm pb
\(\Rightarrow g\left(x\right)=\left|h\left(x\right)\right|\) có 5 cực trị, ngoài cùng bên phải dương => ngoài cùng bên phải là cực tiểu, đan ngược vào trong CT-CĐ-CT-CĐ-CT => 3 cực tiểu và 2 cực đại
Đúng 2
Bình luận (3)
