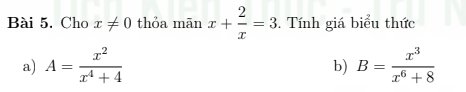a:
\(x+\dfrac{2}{x}=3\)
=>\(\left(x+\dfrac{2}{x}\right)^2=3^2=9\)
=>\(x^2+\dfrac{4}{x^2}+2\cdot x\cdot\dfrac{2}{x}=3^2\)
=>\(x^2+\dfrac{4}{x^2}=9-4=5\)
\(A=\dfrac{x^2}{x^4+4}=1:\left(\dfrac{x^4+4}{x^2}\right)=1:\left(x^2+\dfrac{4}{x^2}\right)=\dfrac{1}{5}\)
b: \(x+\dfrac{2}{x}=3\)
=>\(\left(x+\dfrac{2}{x}\right)^3=3^3=27\)
=>\(x^3+3\cdot x^2\cdot\dfrac{2}{x}+3\cdot x\cdot\left(\dfrac{2}{x}\right)^2+\left(\dfrac{2}{x}\right)^3=27\)
=>\(x^3+\dfrac{8}{x^3}+6x+\dfrac{12}{x}=27\)
=>\(x^3+\dfrac{8}{x^3}+6\left(x+\dfrac{2}{x}\right)=27\)
=>\(x^3+\dfrac{8}{x^3}+6\cdot3=27\)
=>\(x^3+\dfrac{8}{x^3}=27-18=9\)
\(B=\dfrac{x^3}{x^6+8}=1:\dfrac{x^6+8}{x^3}=1:\left(x^3+\dfrac{8}{x^3}\right)=1:9=\dfrac{1}{9}\)