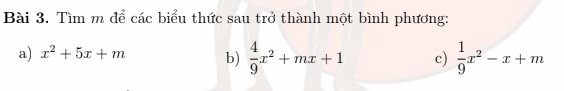a: \(x^2+5x+m=x^2+2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+m-\dfrac{25}{4}\)
\(=\left(x+\dfrac{5}{2}\right)^2+m-\dfrac{25}{4}\)
Để biểu thức này trở thành bình phương thì \(m-\dfrac{25}{4}=0\)
=>\(m=\dfrac{25}{4}\)
b: \(\dfrac{4}{9}x^2+mx+1\)
\(=\left(\dfrac{2}{3}x\right)^2+1^2\pm2\cdot\dfrac{2}{3}x\cdot1+mx\pm\dfrac{4}{3}x\)
\(=\left(\dfrac{2}{3}x\pm1\right)^2+x\left(m\pm\dfrac{4}{3}\right)\)
Để biểu thức trở thành bình phương thì \(m\pm\dfrac{4}{3}=0\)
=>\(\left[{}\begin{matrix}m+\dfrac{4}{3}=0\\m-\dfrac{4}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{4}{3}\\m=\dfrac{4}{3}\end{matrix}\right.\)
c: \(\dfrac{1}{9}x^2-x+m=\left(\dfrac{1}{3}x\right)^2-2\cdot\dfrac{1}{3}x\cdot\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+m-\dfrac{9}{4}\)
\(=\left(\dfrac{1}{3}x-\dfrac{3}{2}\right)^2+m-\dfrac{9}{4}\)
Để biểu thức trở thành bình phương thì \(m-\dfrac{9}{4}=0\)
=>\(m=\dfrac{9}{4}\)