\(g'\left(x\right)=2f\left(f^2\left(x\right)-2022m\right).f'\left(f^2\left(x\right)-2022m\right).2f\left(x\right).f'\left(x\right)\)
Từ đồ thị \(f\left(x\right)\ge0;\forall x\) nên \(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f^2\left(x\right)-2022m\right)=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1;0;1\\f^2\left(x\right)-2022m=-1;0;1\end{matrix}\right.\)
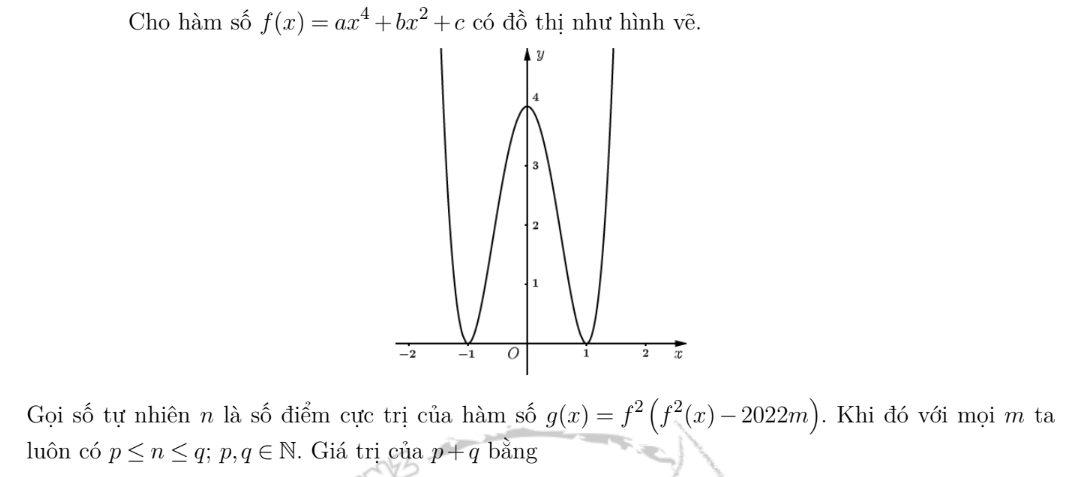
Nghịch suy \(f\left(x\right)=\left(2x^2-2\right)^2\Rightarrow f^2\left(x\right)-2022m=\left(2x^2-2\right)^4-2022m=h\left(x\right)\)
Hàm h(x) dạng y hệt hàm f(x), với 3 cực trị là \(\left(-1;-2022m\right);\left(0;16-2022m\right);\left(1;-2022m\right)\)
3 đường -1;0;1 cắt đồ thị h(x) tại tối thiểu 0 điểm và tối đa 12 điểm
\(\Rightarrow g\left(x\right)\) có từ 3 tới 15 cực trị