\(f\left(x\right)=ax^3+bx^2+cx+d\)
Đồ thị có 2 điểm cực trị tại \(x=1;x=2021\) và có dạng chữ N hoặc M nên đồ thị hàm số cắt trục hoành ít nhất 3 điểm phân biệt
\(f\left(x\right)=f\left(m\right)\Rightarrow f\left(x\right)-f\left(m\right)=0\) phương trình này có nghiệm khi và chỉ khi đồ thị hàm số \(y=f\left(x\right)\) cắt đường thẳng \(y=f\left(m\right)\) tại ít nhất một điểm.
Để phương trình \(f\left(x\right)=f\left(m\right)\) có 3 nghiệm phân biệt, đường thẳng \(y=f\left(m\right)\)) phải cắt đồ thị hàm số \(y=f\left(x\right)\) tại đúng 3 điểm phân biệt.
Vì hàm số \(f\left(x\right)\) có hai điểm cực trị tại \(x=1\) và \(x=2021\), nên giá trị của m phải nằm trong khoảng giữa 1 và 2021. Do m là số nguyên nên ta có \(\text{2021−1−1=2019}\) (giá trị nguyên của m thỏa mãn). Chọn B
Giả sử \(a>0\) (với \(a< 0\) hoàn toàn giống nhau về cách làm và kết quả)
Ta có BBT của \(f\left(x\right)\)
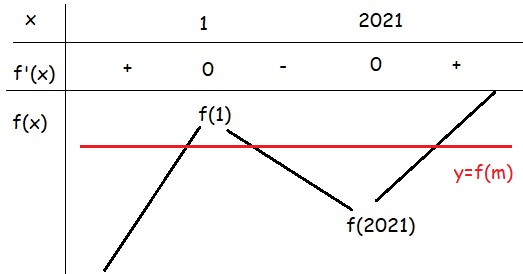
Từ BBT ta thấy \(f\left(x\right)=f\left(m\right)\) có 3 nghiệm pb \(\Rightarrow f\left(2021\right)< f\left(m\right)< f\left(1\right)\)
Mặt khác do hàm \(f\left(x\right)\) nghịch biến trên \(\left(1,2021\right)\)
\(\Rightarrow\Rightarrow f\left(2021\right)< f\left(m\right)< f\left(1\right)\Leftrightarrow1< m< 2021\)
\(\Rightarrow\) Có \(2020-2+1=2019\) giá trị nguyên của m












