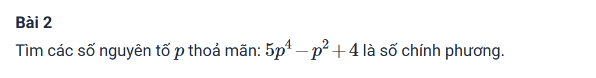Đặt \(n=5p^4-p^2+4\)
- Với \(p=3\Rightarrow n=400=20^2\) thỏa mãn
- Với \(p\ne3\Rightarrow p\) ko chia hết cho 3
\(\Rightarrow p^2\) chia 3 dư 1
\(\Rightarrow2p^2-1\) chia 3 dư 1
\(\Rightarrow p^2\left(2p^2-1\right)\) chia 3 dư 1
\(\Rightarrow n=3\left(p^4+1\right)+p^2\left(2p^2-1\right)+1\) chia 3 dư 2
\(\Rightarrow\) n không là SCP (do SCP chia 3 chỉ dư 0 hoặc 1)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (2)
