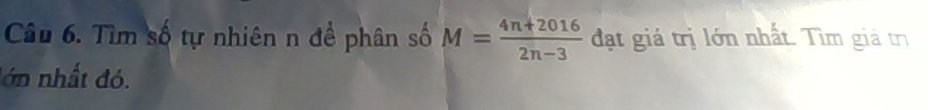\(M=\dfrac{4n+2016}{2n-3}\left(n\in N\right)\)
\(\Rightarrow M=\dfrac{4n-6+6+2016}{2n-3}\)
\(\Rightarrow M=\dfrac{2\left(2n-3\right)+2022}{2n-3}\)
\(\Rightarrow M=2+\dfrac{2022}{2n-3}\)
mà \(2n\ge0\Rightarrow2n-3\ge-3\Rightarrow\dfrac{2022}{2n-3}\le-\dfrac{2022}{3}=-674\left(n=0\right)\)
\(\Rightarrow M=2+\dfrac{2022}{2n-3}\le2-674=-672\)
Vậy \(GTLN\left(M\right)=-672\left(n=0\right)\)
Đề bài là GTLN nhưng k có GTLN mà sửa lại đề bài là tìm GTNN= 2-674=-672, tại n=0, thay dấu <= thành dấu >= là được.
\(M=2+\dfrac{2022}{2n-3}\)
M lớn nhất khi \(\dfrac{2022}{2n-3}\) lớn nhất
\(\Rightarrow2n-3\) là số nguyên dương nhỏ nhất
\(\Rightarrow2n-3=1\)
\(\Rightarrow n=2\)
Vậy với \(n=2\) thì \(M\) đạt giá trị lớn nhất là \(M=2024\)