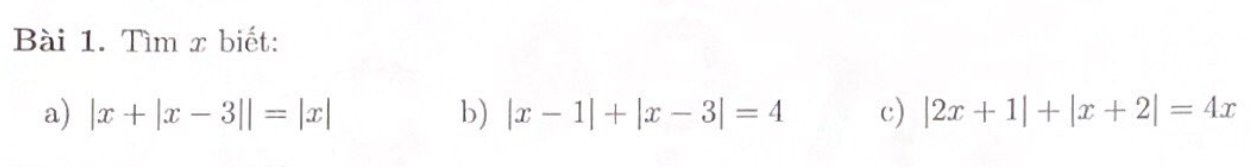a: |x+|x-3||=|x|
=>\(\left[{}\begin{matrix}x+\left|x-3\right|=x\\x+\left|x-3\right|=-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left|x-3\right|=0\\\left|x-3\right|=-2x\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x-3=0\\\left\{{}\begin{matrix}-2x>=0\\\left(x-3\right)^2=\left(-2x\right)^2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\\left\{{}\begin{matrix}x< =0\\\left(2x-x+3\right)\left(2x+x-3\right)=0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\\left\{{}\begin{matrix}x< =0\\\left(x+3\right)\left(3x-3\right)=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
c: TH1: \(x< -2\)
Phương trình sẽ trở thành:
\(-2x-1-x-2=4x\)
=>4x=-3x-3
=>7x=-3
=>\(x=-\dfrac{3}{7}\left(loại\right)\)
TH2: \(-2< =x< -\dfrac{1}{2}\)
Phương trình sẽ trở thành:
\(x+2-2x-1=4x\)
=>4x=-x+1
=>5x=1
=>\(x=\dfrac{1}{5}\left(loại\right)\)
TH3: x>=-1/2
Phương trình sẽ trở thành:
4x=x+2+2x+1
=>4x=3x+3
=>x=3(nhận)
b: TH1: x<1
Phương trình sẽ trở thành:
\(1-x+3-x=4\)
=>4-2x=4
=>2x=0
=>x=0(nhận)
TH2: 1<=x<3
Phương trình sẽ trở thành:
\(x-1+3-x=4\)
=>2=4(loại)
TH3: x>=3
Phương trình sẽ trở thành:
x-1+x-3=4
=>2x=8
=>x=4(nhận)