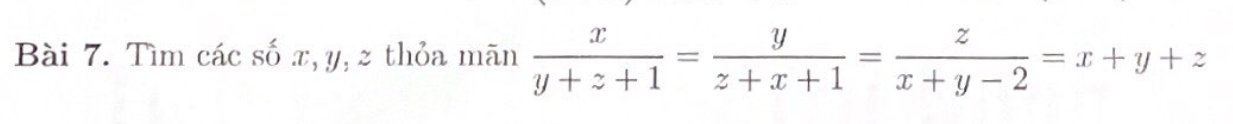TH1: \(x+y+z=0\Rightarrow\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=0\)
\(\Rightarrow x=y=z=0\)
TH2: \(x+y+z\ne0\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(x+y+z=\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=\dfrac{1}{2}\\\dfrac{x}{y+z+1}=\dfrac{1}{2}\\\dfrac{y}{z+x+1}=\dfrac{1}{2}\\\dfrac{z}{x+y-2}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=\dfrac{1}{2}\\2x=y+z+1\\2y=z+x+1\\2z=x+y-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=\dfrac{1}{2}\\3x=x+y+z+1=\dfrac{1}{2}+1=\dfrac{3}{2}\\3y=x+y+z+1=1+\dfrac{1}{2}=\dfrac{3}{2}\\3z=x+y+z-2=\dfrac{1}{2}-2=-\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)