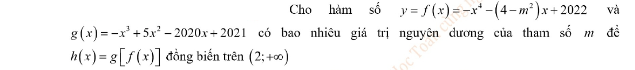Bài này chỉ có 1 TH thôi, do \(f'\left(x\right)=-4x^3-4+m^2=0\) luôn có nghiệm duy nhất \(x=\sqrt[3]{\dfrac{m^2-4}{4}}\) với mọi m
Hơn nữa \(g\left(x\right)\) ko có cực trị nên vấn đề còn đơn giản nữa: cực trị của \(h\left(x\right)\) là cực trị của \(f\left(x\right)\) luôn
Dẫn tới \(\sqrt[3]{\dfrac{m^2-4}{4}}\le2\) xong chuyện, ko cần BBT ko cần vẽ gì nhìn cái ra luôn vấn đề
Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh S x q của hình nón là:
Khối hai mươi mặt đều thuộc loại nào sau đây?
A. 3 ; 4
B. 4 ; 3
C. 3 ; 5
D. 5 ; 3
các anh chị giải hộ em câu này nhé :
98769:2,5 với ạ
em cả ơn Ò w Ó
Trong các hàm số sau, hàm số nào đồng biến trên R?
A. y = 2 3 x
B. y = 2 3 x
C. y = 0 , 99 x
D. y = 2 - 3 x
Phương trình 2 ( 2 x 2 - 3 x + 1 ) = 1 có bao nhiêu nghiệm?
A. 0
B. 2
C. 3
D.. 1
Cho hàm số y = x 4 + 3 x có giá trị cực đại y 1 và giá trị cực tiểu y 2 . Giá trị của S = y 1 - y 2 bằng
A. S = 8
B. S = 0
C. S = -2
D. S = -8
Ông An gửi ngân hàng 150 triệu đồng với lãi suất 0,8%/tháng, sau mỗi tháng tiền lãi được nhập vào vốn (lãi kép). Hỏi sau một năm số tiền lãi ông An thu được gần nhất với kết quả nào sau đây.
A. 15.050.000 đồng
B. 165.050.000 đồng
C. 165.051.000 đồng
D. 15.051.000 đồng
Tính tích phân I = ∫ 1 2 e ln 2 x + 1 x d x .
A. I = 1 3 l n 3 x + l n x
B. I = 1 3 l n 3 2 + l n 2 2 + 2 ln 2 + 4 3
C. ln 2 2 + 1 3
D. I = 1 3 l n 3 2 + l n 2 2 + 2 ln 2 + 1
Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.
A. M = (-3;4)
B. M = (3;-4)
C. M = (-3;-4)
D. M = (1;-3)
