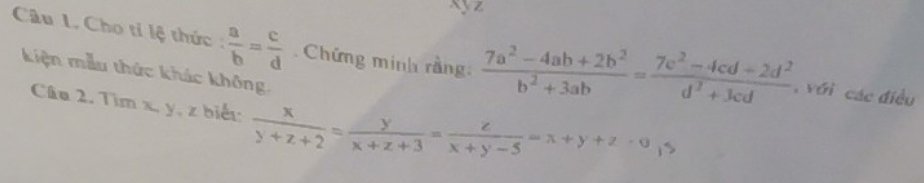Câu 1 :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=k^2\)
Ta có :
\(\dfrac{7a^2-4ab+2b^2}{b^2+3ab}=\dfrac{b^2\left(7\dfrac{a^2}{b^2}-4\dfrac{a}{b}+2\right)}{b^2\left(1+3\dfrac{a}{b}\right)}=\dfrac{7k^2-4k+2}{1+3k}\left(1\right)\)
\(\dfrac{7c^2-4cd+2d^2}{c^2+3cd}=\dfrac{c^2\left(7\dfrac{c^2}{d^2}-4\dfrac{c}{d}+2\right)}{c^2\left(1+3\dfrac{c}{d}\right)}=\dfrac{7k^2-4k+2}{1+3k}\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{7a^2-4ab+2b^2}{b^2+3ab}=\dfrac{7c^2-4cd+2d^2}{c^2+3cd}\left(đpcm\right)\)
Đúng 1
Bình luận (0)
