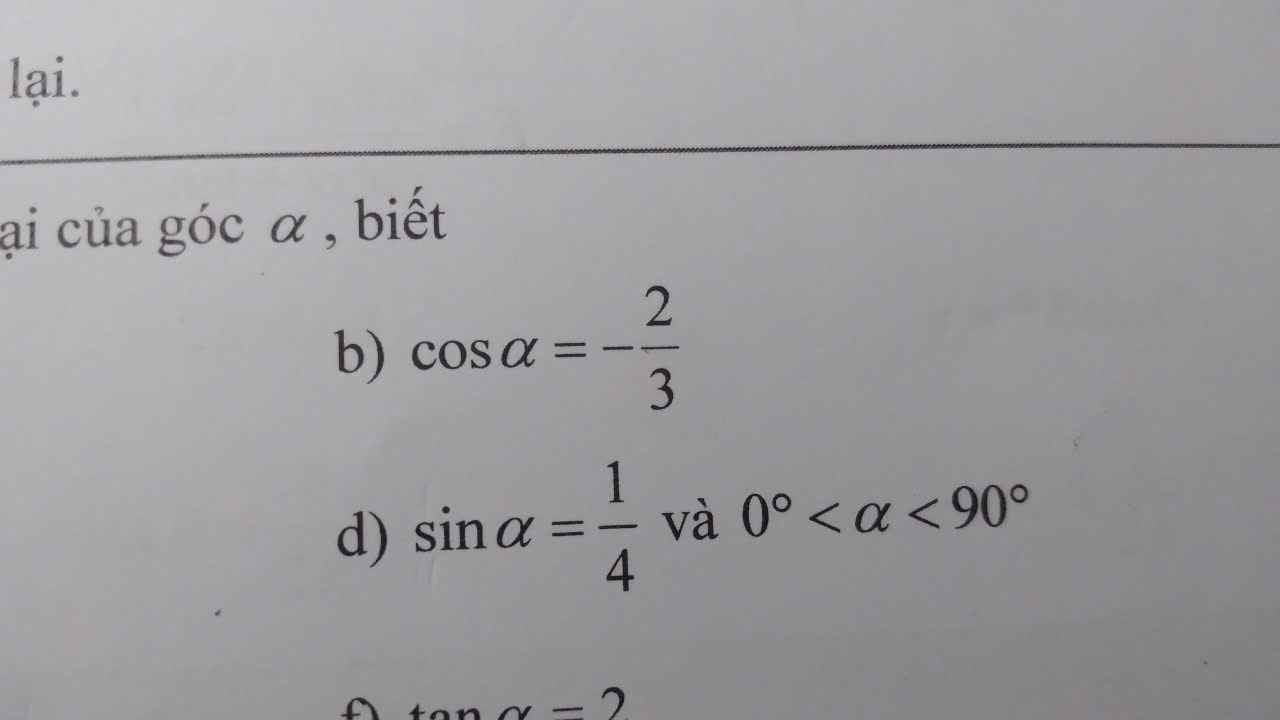b: \(cos^2\alpha+sin^2\alpha=1\)
=>\(sin^2\alpha=1-\left(-\dfrac{2}{3}\right)^2=\dfrac{5}{9}\)
=>\(\left[{}\begin{matrix}sin\alpha=\dfrac{\sqrt{5}}{3}\\sin\alpha=-\dfrac{\sqrt{5}}{3}\end{matrix}\right.\)
TH1: \(sin\alpha=\dfrac{\sqrt{5}}{3}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\sqrt{5}}{3}:\dfrac{-2}{3}=-\dfrac{\sqrt{5}}{2}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=-\dfrac{2}{\sqrt{5}}\)
TH2: \(sin\alpha=-\dfrac{\sqrt{5}}{3}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=-\dfrac{\sqrt{5}}{3}:\dfrac{-2}{3}=\dfrac{\sqrt{5}}{2}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=1:\dfrac{\sqrt{5}}{2}=\dfrac{2}{\sqrt{5}}\)
d:\(0^0< \alpha< 90^0\)
=>\(cos\alpha>0\)
=>\(cos\alpha=\sqrt{1-\left(\dfrac{1}{4}\right)^2}=\sqrt{\dfrac{15}{16}}=\dfrac{\sqrt{15}}{4}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{4}:\dfrac{\sqrt{15}}{4}=\dfrac{\sqrt{15}}{15}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=1:\dfrac{\sqrt{15}}{15}=\sqrt{15}\)