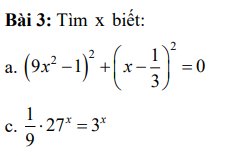a: \(\left(9x^2-1\right)^2+\left(x-\dfrac{1}{3}\right)^2=0\)
=>\(\left[9\left(x^2-\dfrac{1}{9}\right)\right]^2+\left(x-\dfrac{1}{3}\right)^2=0\)
=>\(81\left(x-\dfrac{1}{3}\right)^2\left(x+\dfrac{1}{3}\right)^2+\left(x-\dfrac{1}{3}\right)^2=0\)
=>\(\left(x-\dfrac{1}{3}\right)^2\left[81\left(x+\dfrac{1}{3}\right)^2+1\right]=0\)
mà \(81\left(x+\dfrac{1}{3}\right)^2+1>=1>0\forall x\)
nên \(x-\dfrac{1}{3}=0\)
=>\(x=\dfrac{1}{3}\)
c: \(\dfrac{1}{9}\cdot27^x=3^x\)
=>\(\left(\dfrac{3}{27}\right)^x=\dfrac{1}{9}\)
=>\(\left(\dfrac{1}{9}\right)^x=\dfrac{1}{9}\)
=>x=1
Đúng 1
Bình luận (0)
