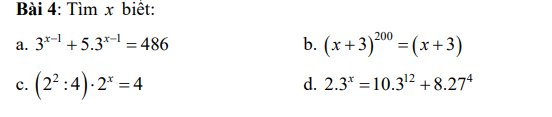\(a,3^{x-1}+5\cdot3^{x-1}=486\\ 3^{x-1}\cdot\left(1+5\right)=486\\ 3^{x-1}\cdot6=486\\ 3^{x-1}=486:6\\ 3^{x-1}=81\\ 3^{x-1}=3^4\\ x-1=4\\ x=1+4\\ x=5\\ b,\left(x+3\right)^{200}=\left(x+3\right)\\ \left(x+3\right)^{200}-\left(x+3\right)=0\\ \left(x+3\right)\left[\left(x+3\right)^{199}-1\right]=0\\ TH1:x+3=0\\ x=-3\\ TH2:\left(x+3\right)^{199}-1=0\\ \left(x+3\right)^{199}=1\\ \left(x+3\right)^{199}=1^{199}\\ x+3=1\\ x=1-3\\ x=-2\)
a)
\(3^{x-1}+5.3^{x-1}=486\\
\Rightarrow3^{x-1}.\left(1+5\right)=486\\
\Rightarrow3^{x-1}.6=486\\
\Rightarrow3^{x-1}=486:6\\
\Rightarrow3^{x-1}=81\\
\Rightarrow3^{x-1}=3^4\\
\Rightarrow x-1=4\\
\Rightarrow x=5\)
Vậy...
b)
\(\left(x+3\right)^{200}=\left(x+3\right)\\
\Rightarrow\left(x+3\right)^{200}-\left(x+3\right)=0\\
\Rightarrow\left(x+3\right).\left[\left(x+3\right)^{199}-1\right]=0\\
\Rightarrow\left[{}\begin{matrix}x+3=0\\\left(x+3\right)^{199}-1=0\end{matrix}\right.\\
\Rightarrow\left[{}\begin{matrix}x=-3\\\left(x+3\right)^{199}=1\end{matrix}\right.\\
\Rightarrow\left[{}\begin{matrix}x=-3\\x+3=1\end{matrix}\right.\\
\Rightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
Vậy...
c)
\(\left(2^2:4\right).2^x=4\\
\Rightarrow\left(4:4\right).2^x=2^2\\
\Rightarrow1.2^x=2^2\\
\Rightarrow2^x=2^2\\
\Rightarrow x=2\)
Vậy...
d)
\(2.3^x=10.3^{12}+8.27^4\\
\Rightarrow2.3^x=10.3^{12}+8.3^{12}\\
\Rightarrow2.3^x=3^{12}.\left(10+8\right)\\
\Rightarrow2.3^x=3^{12}.18\\
\Rightarrow3^x=3^{12}.18:2\\
\Rightarrow3^x=3^{12}.9\\
\Rightarrow3^x=3^{12}.3^2\\
\Rightarrow3^x=3^{14}\\
\Rightarrow x=14\)
Vậy...
\(c,\left(2^2:4\right)\cdot2^x=4\\ \left(4:4\right)\cdot2^x=2^2\\ 2^x=2^2\\ x=2\\ d,2\cdot3^x=10\cdot3^{12}+8\cdot27^4\\ 2\cdot3^x=10\cdot3^{12}+8\cdot\left(3^3\right)^4\\ 2\cdot3^x=10\cdot3^{12}+8\cdot3^{12}\\ 2\cdot3^x=3^{12}\cdot\left(10+8\right)\\ 2\cdot3^x=3^{12}\cdot18\\ 2\cdot3^x=3^{14}\cdot2\\ 3^x=3^{14}\\ x=14\)