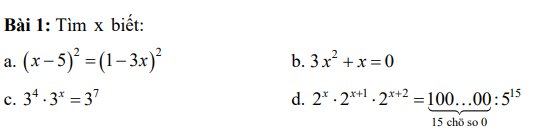`c, 3^4 . 3^x = 3^7`
`=> 3^x = 3^7 : 3^4`
`=> 3^x = 3^3`
`=> x=3`
Vậy: `x=3`
`d, 2^x. 2^(x+1) . 2^(x+2) = \underbrace(100...00)_(15 chữ số0) : 5^15`
`=> 2^x . 2^x . 2 . 2^x . 4 = 10^15 : 5^15`
`=> 2^x . 2^x . 2^x . 2^3 = 2^15`
`=> 2^(3x) = 2^15 : 2^3`
`=> 2^(3x) = 2^12`
`=> 3x = 12`
`=> x=4`
Vậy: `x=4`
`a, (x - 5)^2 = (1 - 3x)^2`
`=> (x - 5)^2 - (1 - 3x)^2= 0`
`=> (x - 5 - 1 + 3x)(x - 5 + 1 - 3x) = 0`
`=> (4x - 6)(-2x -4)=0`
`=> [(4x - 6= 0),(-2x - 4= 0):}`
`=> [(4x = 6),(-2x = 4):}`
`=> [(x = 3/2),(x = -2):}`
Vậy: `x=3/2;x=-2`
`b, 3x^2 +x = 0`
`=> x . 3x + x . 1 = 0`
`=> x . (3x+1)=0`
`=> [(x=0),(3x+1=0):}`
`=> [(x=0),(3x=-1):}`
`=> [(x=0),(x=-1/3):}`
Vậy: `x = 0 ; x=-1/3`