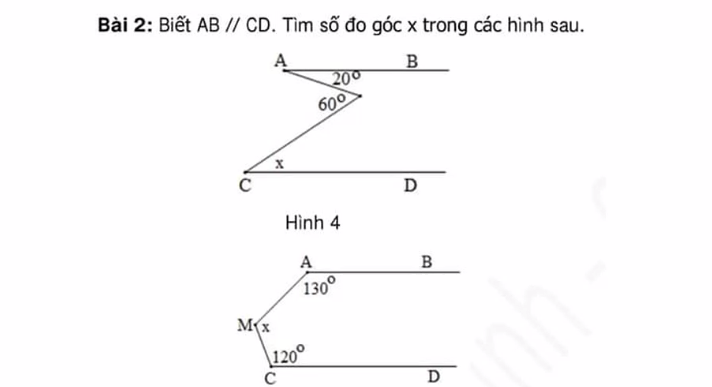
a:
Vẽ lại hình:
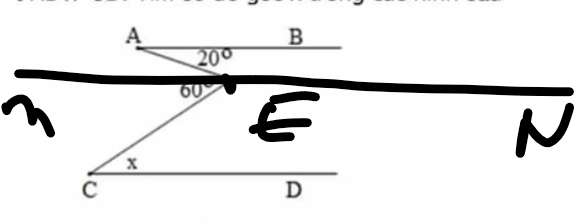
Kẻ EM//AB//CD, EM và AB nằm khác phía so với đoạn thẳng AE
EM//AB
=>\(\widehat{MEA}=\widehat{EAB}\)(hai góc so le trong)
=>\(\widehat{MEA}=20^0\)
Ta có: \(\widehat{MEA}+\widehat{MEC}=\widehat{AEC}\)
=>\(\widehat{MEC}+20^0=60^0\)
=>\(\widehat{MEC}=40^0\)
Ta có: EM//CD
=>\(\widehat{MEC}=\widehat{DCE}\)(hai góc so le trong)
=>\(x=40^0\)
b:
Vẽ lại hình:
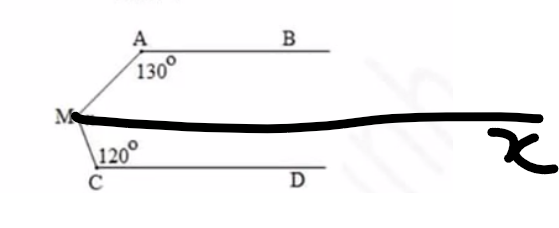
Kẻ Mx//AB//CD(Mx và AB nằm cùng phía so với đoạn thẳng MA)
Mx//AB
=>\(\widehat{xMA}+\widehat{MAB}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{xMA}+130^0=180^0\)
=>\(\widehat{xMA}=50^0\)
Ta có: Mx//CD
=>\(\widehat{xMC}+\widehat{C}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{xMC}+120^0=180^0\)
=>\(\widehat{xMC}=60^0\)
\(x=\widehat{AMC}=\widehat{xMA}+\widehat{xMC}=60^0+50^0=110^0\)