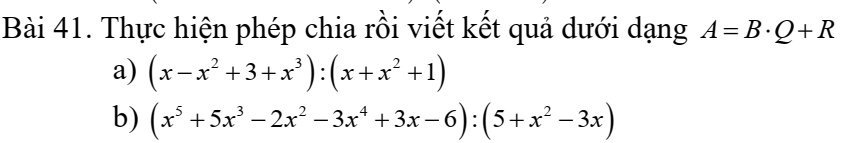a: \(\dfrac{x-x^2+3+x^3}{x+x^2+1}\)
\(=\dfrac{x^3-x^2+x+3}{x^2+x+1}\)
\(=\dfrac{x^3+x^2+x-2x^2-2x-2+2x+5}{x^2+x+1}\)
\(=x-2+\dfrac{2x+5}{x^2+x+1}\)
=>\(x^3-x^2+x+3=\left(x-2\right)\left(x^2+x+1\right)+\left(2x+5\right)\)
b: \(\dfrac{x^5+5x^3-2x^2-3x^4+3x-6}{5+x^2-3x}\)
\(=\dfrac{x^5-3x^4+5x^3-2x^2+3x-6}{x^2-3x+5}\)
\(=\dfrac{x^3\left(x^2-3x+5\right)-2x^2+6x-10-3x+4}{x^2-3x+5}\)
\(=x^3-2+\dfrac{-3x+4}{x^2-3x+5}\)
=>\(x^5-3x^4+5x^3-2x^2+3x-6=\left(x^3-2\right)\left(x^2-3x+5\right)+\left(-3x+4\right)\)
Đúng 2
Bình luận (0)
