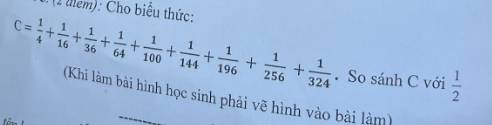\(C=\dfrac{1}{4}+\dfrac{1}{16}+...+\dfrac{1}{324}\)
\(=\dfrac{1}{4}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{9^2}\right)\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{9^2}< \dfrac{1}{8\cdot9}=\dfrac{1}{8}-\dfrac{1}{9}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}< 1-\dfrac{1}{9}\)
=>\(1+\dfrac{1}{2^2}+...+\dfrac{1}{9^2}< 2-\dfrac{1}{9}\)
=>\(C=\dfrac{1}{4}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{9^2}\right)< \dfrac{1}{4}\left(2-\dfrac{1}{9}\right)\)
=>\(C< \dfrac{1}{2}-\dfrac{1}{36}\)
=>\(C< \dfrac{1}{2}\)
Nhìn nó dễ khi mà bài này phải " CMR C < \(\dfrac{1}{2}\) hoặc C > \(\dfrac{1}{2}\) " thì mik làm dc chứ cái này mik chịu gòi ^^