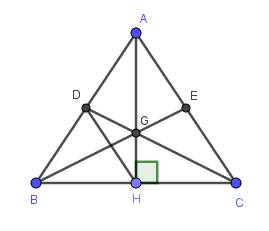
a) Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow AB=AC\)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:
\(AH\) là cạnh chung
\(AB=AC\left(cmt\right)\)
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)
b) Do \(HD\) // \(AC\left(gt\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{CAH}\) (so le trong)
Mà \(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{BAH}\)
\(\Rightarrow\widehat{AHD}=\widehat{DAH}\)
\(\Rightarrow\Delta ADH\) cân tại D
c) Do HD // AC (gt)
\(\Rightarrow\widehat{DHB}=\widehat{ACB}\)
Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow\widehat{ACB}=\widehat{ABC}\)
\(\Rightarrow\widehat{DHB}=\widehat{ABC}\)
\(\Rightarrow\widehat{DHB}=\widehat{DBH}\)
\(\Rightarrow\Delta DBH\) cân tại D
\(\Rightarrow DH=DB\) (1)
Do \(\Delta ADH\) cân tại D (cmt)
\(\Rightarrow AD=DH\) (2)
Từ (1) và (2) \(\Rightarrow AD=DB\)
\(\Rightarrow D\) là trung điểm của AB
\(\Rightarrow CD\) là đường trung tuyến của \(\Delta ABC\)
Do \(AH\) là đường cao của \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow AH\) là đường trung tuyến của \(\Delta ABC\)
Do \(E\) là trung điểm của AC (gt)
\(\Rightarrow BE\) là đường trung tuyến của \(\Delta ABC\)
Mà \(G\) là giao điểm của \(AH\) và \(CD\) (gt)
\(\Rightarrow G\) là trọng tâm của \(\Delta ABC\)
Mà \(BE\) là đường trung tuyến của \(\Delta ABC\) (cmt)
\(\Rightarrow B,G,E\) thẳng hàng














