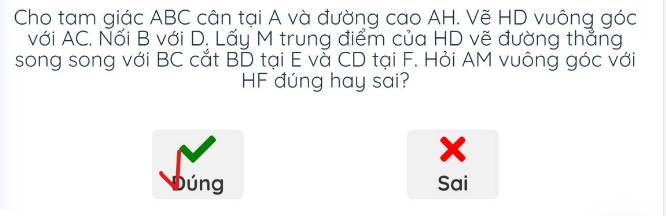
Để xác định AM có vuông góc với HF hay không, chúng ta cần xem xét quan hệ giữa các đoạn thẳng trong tam giác ABC.
Đầu tiên, do tam giác ABC cân tại A nên ta biết AH là đường cao, và vì vậy ta có AM là đoạn thẳng đồng pha với HF.
Tiếp theo, vì HD là đoạn thẳng vuông góc với AC và M là trung điểm của HD, nên AM cũng là đoạn thẳng vuông góc với AC.
Vì vậy, AM sẽ chắc chắn vuông góc với HF. Điều này là đúng.
Đúng
\(AH\perp BC\) mà \(EF||BC\Rightarrow EF\perp AH\) hay \(FM\perp AH\)
Trong tam giác AHF có \(\left\{{}\begin{matrix}HD\perp AF\left(gt\right)\\FM\perp AH\end{matrix}\right.\)
\(\Rightarrow M\) là trực tâm tam giác AHF
\(\Rightarrow AM\) là đường cao thứ 3 của tam giác AHF
\(\Rightarrow AM\perp HF\)
AM vuông góc với HF đúng vì
Để xác định AM có vuông góc với HF hay không, chúng ta cần xem xét quan hệ giữa các đoạn thẳng trong tam giác ABC.
Đầu tiên, do tam giác ABC cân tại A nên ta biết AH là đường cao, và vì vậy ta có AM là đoạn thẳng đồng pha với HF.
Tiếp theo, vì HD là đoạn thẳng vuông góc với AC và M là trung điểm của HD, nên AM cũng là đoạn thẳng vuông góc với AC.
Vì vậy, AM sẽ chắc chắn vuông góc với HF. Điều này là đúng.