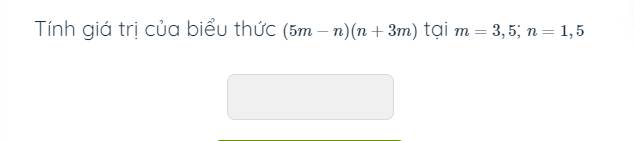1: \(\left(4x^2-\dfrac{1}{2}\right)\left(16x^4+2x^2+\dfrac{1}{4}\right)\)
\(=\left(4x^2-\dfrac{1}{2}\right)\left[\left(4x^2\right)^2+4x^2\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]\)
\(=\left(4x^2\right)^3-\left(\dfrac{1}{2}\right)^3=64x^6-\dfrac{1}{8}\)
2: \(P\left(x\right)+Q\left(x\right)\)
\(=7x^4+5x^3+8x^2-\dfrac{1}{3}+x^4-3x^3+8x^2-5x-\dfrac{2}{3}\)
\(=8x^4+2x^3+16x^2-5x-1\)
3: M(x)-N(x)
\(=3x^4-2x^3+5x^2-4x+1+3x^4-2x^3+3x^2-7x-5\)
\(=6x^4-4x^3+8x^2-11x-4\)
4: Khi m=3,5 và n=1,5 thì
\(\left(5m-n\right)\left(n+3m\right)=\left(5\cdot3,5-1,5\right)\left(1,5+3\cdot3,5\right)\)
\(=16\cdot12=192\)
5: \(\left(x+y\right)\cdot\dfrac{h}{2}\)