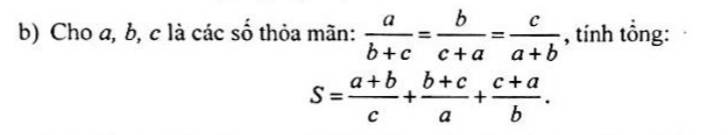Question

Answer 1

Áp dụng TCDTSBN, ta có :

\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{b+c+c+a+a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{c}{a+b}=\dfrac{1}{2}\\\dfrac{a}{b+c}=\dfrac{1}{2}\\\dfrac{b}{c+a}=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a+b}{c}=2\\\dfrac{b+c}{a}=2\\\dfrac{c+a}{b}=2\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}=2+2+2=6\)

Vậy \(S=\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}=6\)