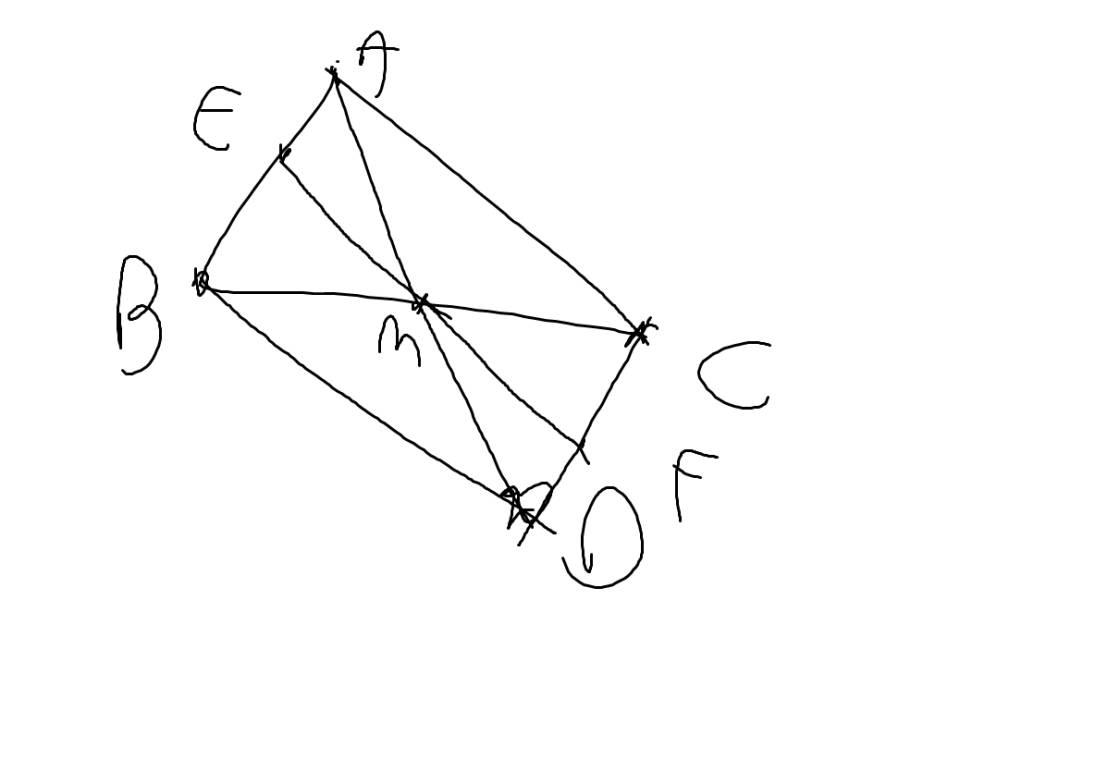
| GT | ΔABC, M là trung điểm của BC, MD=MA AE=DF; \(E\in AB;F\in CD\) |
| KL | a: ΔMAB=ΔMDC b: AB=CD; AB//CD c: ΔABC=ΔDCB d: E,M,F thẳng hàng |
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>AB=DC
Ta có ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
d: Xét ΔMAE và ΔMDF có
MA=MD
\(\widehat{MAE}=\widehat{MDF}\)(hai góc so le trong, AB//CD)
AE=DF
Do đó: ΔMAE=ΔMDF
=>\(\widehat{AME}=\widehat{DMF}\)
mà \(\widehat{AME}+\widehat{DME}=180^0\)(hai góc kề bù)
nên \(\widehat{DMF}+\widehat{DME}=180^0\)
=>E,F,M thẳng hàng














