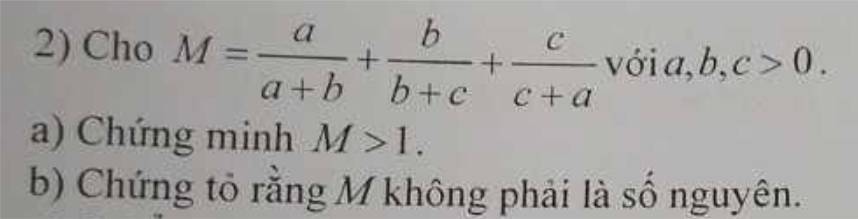Question

Answer 1

Lời giải:

a.

$M> \frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1$

b.

Xét hiệu $\frac{a}{a+b}-\frac{a+c}{a+b+c}=\frac{a(a+b+c)-(a+b)(a+c)}{(a+b)(a+b+c)}=\frac{-a^2}{(a+b)(a+b+c)}<0$ với mọi $a,b,c>0$

$\Rightarrow \frac{a}{a+b}< \frac{a+c}{a+b+c}$

Tương tự với các phân thức còn lại suy ra:

$M< \frac{a+c}{a+b+c}+\frac{b+a}{b+c+a}+\frac{c+b}{a+b+c}=2$

Vậy $1< M< 2$ nên $M$ không là số nguyên.